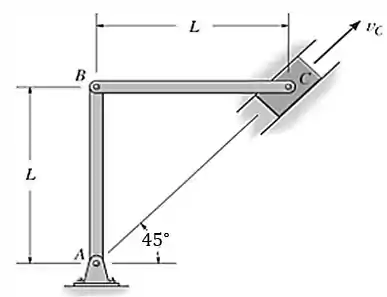
A velocidade do cursor C é de 4 pés/s tubo acima. Determine a velocidade angular das barras AB e BC e a velocidade do ponto B na situação mostrada na figura.
Passo 1
Vamos começar montando a equação da velocidade do ponto :
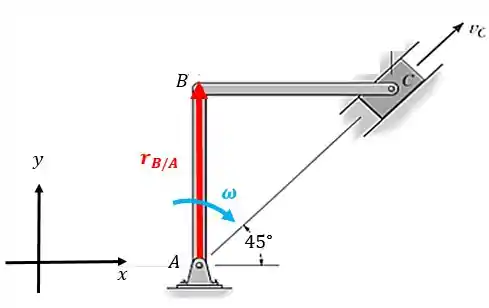
Vamos adotar esses vetores da figura, caso estejam no sentido errado, o resultado vai dar negativo.
O vetor posição será:
E como o nosso sistema de referência adota o sentido anti-horário como positivo, o vetor velocidade angular será negativo, pois faz a barra girar no sentido horário:
Então, nossa equação fica:
O produto vetorial vai ficar assim:
Passo 2
Agora vamos para a barra . Temos que:
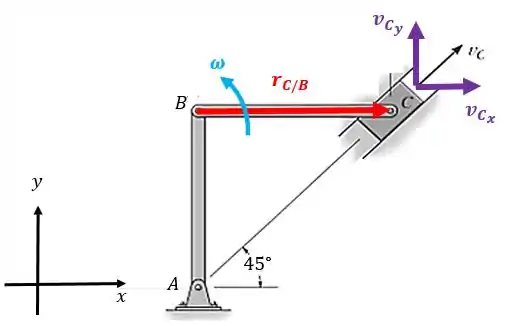
Vamos considerar os vetores como está na figura. Então:
E a velocidade angular da barra é positiva, pois está girando no sentido anti-horário:
Agora vamos decompor o vetor :
Como , temos que:
Beleza?
Agora podemos substituir o que temos na nossa equação da barra :
Vamos resolver o produto vetorial:
Então:
Vamos igualar os termos de mesma componente:
Como deu tudo positivo, significa que escolhemos o sentido correto dos vetores, então a velocidade angular das barras é:
Passo 3
Agora podemos calcular a velocidade do ponto :
E seu módulo é: