Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição entre Planos

Ver Teoria
Exercício 91234567810111213

Enunciado

USP – Álgebra Linear – P2 2021 – Questão 7

Assuma V 3 orientado e considere coordenadas de pontos dados em relação a um sistema de coordenadas fixado em E 3 de base ortonormal e positiva.

Seja r a reta que passa pelo ponto A = - 1,2 , 3 e que é paralela à reta

s : x + y + z = 1 y - z = 2

São equações paramétricas de r :

a) x = - 2 t y = 1 - t z = - 3 + 2 t ,   t ∈ R

b) x = - 2 t y = 2 + t z = - 2 + t ,   t ∈ R

c) x = 2 + t y = 2 + t z = - 2 t ,   t ∈ R

d) x = 1 + 2 t y = - t z = - 1 - t ,   t ∈ R

e) x = - 1 + t y = 2 + t z = 3 - 2 t ,   t ∈ R

f) x = 1 - 2 t y = 1 + t z = 2 + t ,   t ∈ R

Passo 1

Faaaala pessoal! Tudo bem? Tudo bem por aqui também :P

Então vamos lá dar uma olhada nesse problema

Temos uma reta r que passa pelo ponto A = - 1,2 , 3 e que é paralela à reta

s : x + y + z = 1 y - z = 2

Ou seja, o ponto - 1,2 , 3 pertence à reta r , condiz com a equação dela sabe? E também podemos dizer que o vetor diretor de r é o mesmo vetor diretor de s

E aí o nosso objetivo é encontrar as equações paramétricas de r

Gente, só lembrando aqui. Se uma reta p passa pelo ponto ( a , b , c ) e tem o vetor diretor d , e , f , suas equações paramétricas vão ser

x = a + d . t y = b + e . t z = c + f . t ,   t ∈ R

Ou seja, basta termos um ponto da reta r e o seu vetor diretor. Assim, já podemos encontrar suas equações paramétricas 😊

Então vamos lá encontrar essas informações

Passo 2

Vamos dar uma analisada na equação da reta s :

s : x + y + z = 1 y - z = 2

Essa reta é a intersecção dos planos x + y + z = 1 e y - z = 2

Presta atenção nessa informação: se uma reta é a intersecção de 2 planos, o seu vetor diretor vai ser ortogonal aos vetores normais dos planos

OU SEJA: o vetor diretor vai ser o produto vetorial de n 1 e n 2 , os vetores normais dos planos

E só pra lembrar: se temos um plano de equação geral a x + b y + c z + d = 0 , o vetor normal vai ser n = a , b , c

Então, nos planos que se interceptam pra formar a reta s vamos ter

x + y + z = 1 → n 1 = 1,1 , 1

0 x + y - z = 2 → n 2 = 0,1 , - 1

Ebaaa, agora podemos encontrar o vetor diretor de s , que consequentemente é o mesmo de r porque as retas são paralelas

Passo 3

O vetor diretor de s vai ser o produto vetorial dos vetores normais aos 2 planos:

u = 1,1 , 1 × 0,1 , - 1

u = i ^ j ^ k ^ 1 1 1 0 1 - 1

Calculando esse determinante:

u = i ^ j ^ k ^ 1 1 1 0 1 - 1 i ^ j ^ 1 1 0 1 = - i ^ + k ^ - i ^ + j ^ = - 2 i ^ + j ^ + k ^

Lembrando que i ^ é a primeira coordenada, j ^ é a segunda e k ^ é a terceira

Então, o vetor u diretor da reta s vai ser

u = ( - 2,1 , 1 )

Passo 4

Sabemos que a reta r passa pelo ponto A = - 1,2 , 3 e tem o vetor diretor u = ( - 2,1 , 1 )

Então, suas equações paramétricas podem ser escrita assim:

x = - 1 - 2 t y = 2 + 1 t z = 3 + 1 t ,   t ∈ R

Mas pode ser que a alternativa tenha nos dado a equação de outra forma. Ela pode ter colocado OUTRO ponto que pertence à reta e um vetor diretor PARALELO a - 2,1 , 1

Então vamos ver qual delas é condizente com a reta r

Vamos ver o que cada alternativa dá pra gente:

- A letra a dá o ponto 0,1 , - 3 e o vetor diretor - 2 , - 1,2

- A letra b dá o ponto 0,2 , - 2 e o vetor diretor - 2,1 , 1

- A letra c dá o ponto 2,2 , 0 e o vetor diretor 1,1 , - 2

- A letra d dá o ponto 1,0 , - 1 e o vetor diretor 2 , - 1 , - 1

- A letra e dá o ponto - 1,2 , 3 e o vetor diretor 1,1 , - 2

- A letra f dá o ponto ( 1,1 , 2 ) e o vetor diretor - 2,1 , 1

As únicas alternativas em que o vetor diretor é igual ou múltiplo (paralelo) de - 2,1 , 1 são as alternativas B, D e F

Então já podemos descartar as alternativas A, C e E

Passo 5

Então a alternativa que representa a reta r só pode ser B, D ou F. Essas são as equações que têm um vetor diretor condizente com o que encontramos.

Para descobrirmos qual a verdadeira, vamos ver qual delas dá um ponto que pertence a r 😊

- A letra b dá o ponto 0,2 , - 2 :

0 = - 1 - 2 t 2 = 2 + 1 t - 2 = 3 + 1 t → 1 = - 2 t 0 = 1 t - 5 = 1 t

Opa, isso deu um sistema indeterminado. Então o ponto 0,2 , - 2 não pertence à reta r

- A letra d dá o ponto 1,0 , - 1

1 = - 1 - 2 t 0 = 2 + 1 t - 1 = 3 + 1 t → 2 = - 2 t - 2 = 1 t - 4 = 1 t

Isso também deu um sistema impossível. O ponto 1,0 , - 1 não pertence a r .

- A letra f dá o ponto ( 1,1 , 2 )

1 = - 1 - 2 t 1 = 2 + 1 t 2 = 3 + 1 t → 2 = - 2 t - 1 = 1 t - 1 = 1 t

Opa, agora sim! Nas 3 equações, temos que t = - 1 . Então o ponto 1,1 , 2 dá um sistema possível determinado, e portanto pertence à reta r .

Logo, a alternativa correta é a letra F! Essa alternativa dá equações com um ponto pertencente a r e o vetor diretor - 2,1 , 1

Passo 6

Só um spin-off da questão pra vermos geometricamente o que aconteceu hahahaha

A reta r é paralela à reta s . E a reta s é a intersecção desses dois planos:

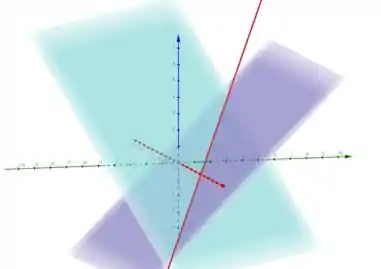
Então s é essa reta vermelha aí ó!

O vetor diretor dessa reta é ortogonal aos vetores normais dos planos:

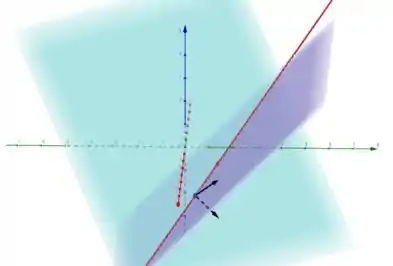
Então a reta r (preta) tem o mesmo vetor diretor. Mas ela passa pelo ponto A = - 1,2 , 3

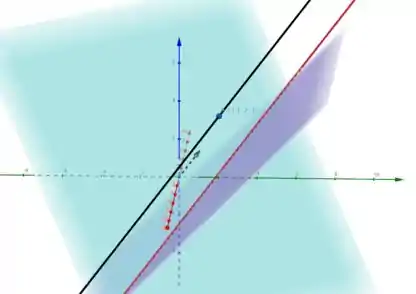
E também passa pelo ponto 1,1 , 2 , como diz a alternativa F 😊

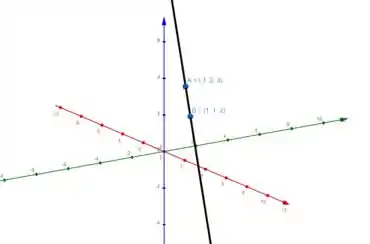
É isso aí galerinha!!

Resposta

f) x = 1 - 2 t y = 1 + t z = 2 + t ,   t ∈ R

Exercícios de Livros Relacionados

Obtenha um vetor normal ao plano π em cada caso:a) π contém A = ( 1 ,1 ,1 ) , B = ( 1 ,0 ,1 ) e C = ( 1 ,2 ,3 ) .b) π : x - 2 y + 4 z + 1 = 0 .c) π : X = 1 ,2 ,0 + λ1 ,- 1 ,1 + μ( 0 ,1 ,- 2 ) .
As equações X = 0,0 , 0 + t α 1,2 , 4 e X = 1,0 , - 2 + t - 1 , - 1 , - 1 , t ∈R , descrevem os movimentos de duas partículas. Determine o valor de α para que haja colisão. Em que instante ela ocorre?
Decomponha o vetor u → = ( - 3 ,4 ,- 5 ) em duas parcelas, uma paralela e outra ortogonal ao plano de equação vetorial X = 1 ,- 2 ,0 + λ- 1 ,0 ,1 + μ( 0 ,0 ,- 1 ) .
O vetor ( 1 ,1 ,m ) é normal ao plano π , que contém a intersecção dos planos π 1 : x - y + z + 1 = 0 e O y z . Determine m e obtenha uma equação geral de π .
Representar graficamente os planos de equações:3 x + 4 y + 2 z - 12 = 0