Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição entre Planos

Ver Teoria
Exercício 71234568910111213

Enunciado

Estude a posição relativa de π 1 e π 2 nos seguintes casos:

  1. π 1 : X = 1 ,   1 ,   1 + λ 0 ,   1 ,   1 + µ - 1 ,   2 ,   1

      π 2 : X = 1 ,   0 ,   0 + λ 1 ,   - 1 ,   0 + µ - 1 ,   - 1 ,   - 2

  2. π 1 : 2 x - y + 2 z - 1 = 0

    π 2 : 4 x - 2 y + 4 z = 0

π 1 : x - y + 2 z - 2 = 0

π 2 : X = 0 ,   0 ,   1 + λ 1 ,   0 ,   3 + µ - 1 ,   1 ,   1

Passo 1

Bora estudar a posição relativa entre planos?!! Vamos nessa, então!!

O enunciado nos dá a equação vetorial dos planos. Mas, aprendemos a ver a posição relativa entre os planos por meio dos coeficientes da equação geral. Então, primeiro teremos que achar a equação geral de cada plano, para depois compararmos os coeficientes.

Passo 2

a Antes de achar as equações gerais dos planos, vamos retirar os dados:

π 1 : A = ( 1 ,   1 ,   1 ) v → = ( 0 ,   1 ,   1 ) u → = ( - 1 ,   2 ,   1 )           e                   π 2 : B = ( 1 ,   0 ,   0 ) r → = ( 1 ,   - 1 ,   0 ) s → = ( - 1 ,   - 1 ,   - 2 )

Montando e resolvendo o produto misto para achar a equação geral de cada plano temos:

Para   π 1 :

- x - y + z + 1 = 0

x + y - z - 1 = 0

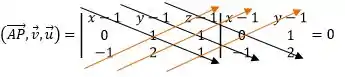
Para   π 2 :

2 x + 2 y - 2 z - 2 = 0

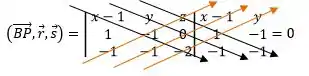
Agora, que temos todos os coeficientes podemos comparar os planos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 1 ,   1 ,   - 1 ,   - 1 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 2 ,   2 ,   - 2 ,   - 2 )

Se   (   a 1 ,   b 1 , c 1 , d 1 ) = α ( a 2 ,   b 2 , c 2 , d 2 ) então os planos são paralelos coincidentes. E, pelos coeficientes que temos:

1 ,   1 ,   - 1 ,   - 1 = 1 2 ( 2 ,   2 ,   - 2 ,   - 2 )

Portanto, os planos são paralelos coincidentes.

Passo 3

b

π 1 : 2 x - y + 2 z - 1 = 0

π 2 : 4 x - 2 y + 4 z = 0

O enunciado já nos dá a equação geral dos planos. Ufa!!! Menos contas!!

Temos que:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 2 ,   - 1 ,   2 ,   - 1 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 4 ,   - 2 ,   4 ,   0 )

Bora comparar os coeficientes!!

Comparando percebemos que:

a 1 ,   b 1 , c 1 = 1 2 ( a 2 ,   b 2 , c 2 )

2 ,   - 1 ,   2 = 1 2 ( 4 ,   - 2 ,   4 )

Já os coeficientes d 1 e d 2 não são proporcionais. Assim, os planos são paralelos distintos.

Passo 4

c

π 1 : x - y + 2 z - 2 = 0

π 2 : X = 0 ,   0 ,   1 + λ 1 ,   0 ,   3 + µ - 1 ,   1 ,   1

Esse item é uma mistura entre os itens a e b . Pois, do plano π 1 foi nos dada a equação geral, já do plano     π 2 temos a equação vetorial. Assim, antes de fazermos qualquer análise teremos que encontrar primeiro a equação geral do plano     π 2 .

Montando e resolvendo o produto misto, temos:

A = 0,0 , 1 ,   v → = 1 ,   0 ,   3 ,   u → = - 1 ,   1 ,   1

- 3 x - 4 y + z - 1 = 0

3 x + 4 y - z + 1 = 0

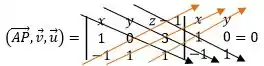
Já que temos todos os coeficientes, basta compararmos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 1 ,   - 1 ,   2 ,   - 2 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 3 ,   + 4 ,   - 1 ,   1 )

Comparando os coeficientes visualmente não conseguimos encontrar nenhuma proporcionalidade comum. Assim, os planos são transversais.

Resposta

a )   P a r a l e l o s   C o i n c i d e n t e s

b )   P a r a l e l o s   D i s t i n t o s

c )   T r a n s v e r s a i s

Exercícios de Livros Relacionados

Obtenha um vetor normal ao plano π em cada caso:a) π contém A = ( 1 ,1 ,1 ) , B = ( 1 ,0 ,1 ) e C = ( 1 ,2 ,3 ) .b) π : x - 2 y + 4 z + 1 = 0 .c) π : X = 1 ,2 ,0 + λ1 ,- 1 ,1 + μ( 0 ,1 ,- 2 ) .
As equações X = 0,0 , 0 + t α 1,2 , 4 e X = 1,0 , - 2 + t - 1 , - 1 , - 1 , t ∈R , descrevem os movimentos de duas partículas. Determine o valor de α para que haja colisão. Em que instante ela ocorre?
Decomponha o vetor u → = ( - 3 ,4 ,- 5 ) em duas parcelas, uma paralela e outra ortogonal ao plano de equação vetorial X = 1 ,- 2 ,0 + λ- 1 ,0 ,1 + μ( 0 ,0 ,- 1 ) .
O vetor ( 1 ,1 ,m ) é normal ao plano π , que contém a intersecção dos planos π 1 : x - y + z + 1 = 0 e O y z . Determine m e obtenha uma equação geral de π .
Representar graficamente os planos de equações:3 x + 4 y + 2 z - 12 = 0