Diga qual é a posição relativa entre planos:
Caso eles forem transversais, determine a equação da reta formada por eles.
Passo 1
Uhh, quando começa com esse “Caso sejam transversais...” já sabemos que tem de chance dos planos serem transversais! Mas, como bons alunos de Geometria Analítica e Álgebra Linear, vamos provar isso!
Para os planos serem transversais, nenhum dos coeficientes pode ser proporcional. Vamos ver se isso “ser” verdade.
Precisamos que
Montando um sisteminha maneiro, obtemos:
Como NENHUM dos bate, nossos planos são de fato transversais.
Passo 2
Pô, mas além de pedir a posição relativa o moço também pediu a equação da reta formada pelos planos!

Calma, galera! É mais fácil do que parece, haha!
Pensa comigo, se dois planos são transversais, eles se cruzam (obviamente, hehe). Quando eles se cruzam forma-se uma reta comum aos dois planos! Ou seja, essa reta contém os únicos pontos em comum entre e !
Se liga nessa figura!
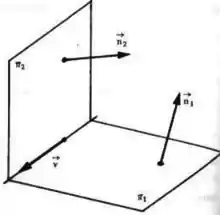
Sacou??
Então, se a gente fizer um sistema com as equações dos planos, vamos achar os pontos em comum entre eles, ou seja, os pontos da reta!
De tiramos que:
De , temos:
Substituindo em :
Logo,
Com isso, nossa reta será formada pelos pontos que satisfazem as relações:
Para escrevermos uma equação paramétrica para a reta precisamos de um vetor diretor e de um ponto da reta. Para isso, vamos pegar dois pontos quaisquer dessa reta e calcular o vetor diretor!
Agora só falta um ponto! Vou usar .
Logo, uma equação paramétrica de é:
FIM 😉