Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pressão Hidrostática

Ver Teoria
Exercício 261234567891011121314151617181920212223242527282930313233

Enunciado

Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 14 – Exercício 31.

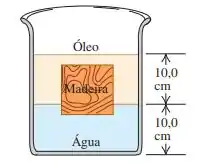
(Cap 14 - Ex 31) Um bloco de madeira cúbico com aresta de 10,0 cm flutua sobre uma interface entre uma camda de água e uma camada de óleo, com uma base situada 1,50 cm abaixo da superfície livre do óleo (Figura 14.34). A densidade do óleo é igual a 790 k g / m 3 . a) Qual é a pressão manométrca na face superior do bloco? b) Qual é a pressão manométrica na face interior do bloco? c) Quais são a massa e a densidade do bloco?

Passo 1

E aí, galera, aqui nesse exercício vamos usar a equação

p - p a t m = ρ g y 2 - y 1 = ρ g h

Para calcular a pressão manométrica nas duas profundidades.

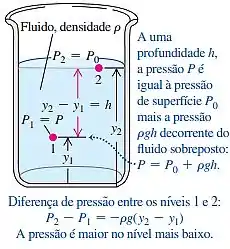
Por teoria sabemos que a pressão varia com a profundidade em um fluido com a densidade uniforme, como mostra a figura a seguir

Passo 2

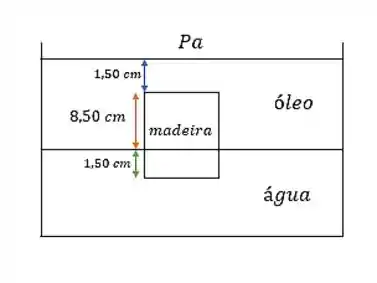
  1. Para facilitar a visualização, vamos desenhar as distancias:

    2. Assim, temos que por teoria a fórmula 14.6 do livro

    Como a face superior fica 1,50 cm abaixo da parte superior do óleo, então

    p - p 0 = ( 7,90 k g / m 3 ) ( 9,80 m / s 2 ) ( 0,0150 m )

    p - p 0 = 116   P a

    Passo 3

  2. A pressão na interface é

    3. p i n t e r f a c e = p a + ρ ó l e o g ( 0,100 m )

    A face inferior do bloco está 1,50 cm abaixo da interface, então a pressão é

    p = p i n t e r f a c e + ρ a g u a g ( 0,0150 m )

    A combinação dessas duas equações fornece

    p - p a = ρ ó l e o g 0,100 m + ρ a g u a g ( 0,0150 m )

    Isso implica que

    p - p a =   [ ( 790   k g / m   ) ( 0.100   m )   +   ( 1000   k g / m   ) ( 0.0150   m ) ] ( 9.80   m / s   )

    p - p a = 921 P a

    Passo 4

  3. Considere as forças no bloco. A área de cada face do bloco é A = 0,100   m 2 = 0,0100   m 2 . Seja a pressão absoluta na face superior p t e a pressão na face inferior seja p b .

Na equação

p = F ⫠ A

usaremos essas pressões para calcular a força exercida pelos fluidos na parte superior e inferior do bloco.

Assim, temos que

∑ F y = m a y

Isso implica que

p b A - p t A - m g = 0

p b - p t A = m g

Note que

p b - p t = p b - p a - p t - p a = 921   P a - 116   P a = 805   P a

a diferença nas pressões absolutas é igual a diferença nas pressões de medida.

Assim,

m = p b - p t A g = ( 805   P a ) ( 0,0100 m 2 ) 9,80 m / s 2 = 0,821 k g

E então

ρ = m V = 0,821 k g 0,100 m 3 = 821 k g / m 3

Resposta

  1. 116   P a
  2. 921 P a
  3. ρ = 821 k g / m 3

Exercícios de Livros Relacionados

Em uma girafa, com a cabeça 2,0m acima do coração e o coração 2,0m acima do solo, a pressão manométrica (hidrostática) do sangue na altura do coração é 250t o r r . Suponha que a girafa está de pé e a
Alguns membros de uma tripulação tentam escapar de um submarino avariado 100m abaixo da superfície. Que força deve ser aplicada a uma escotilha, de 1,20m ×0,6m , para empurrá-la para fora a essa profu
Um grande aquário de 5 m de altura está cheio de água doce até uma altura de 2 m . Uma das paredes do aquário é feita de plástico e tem 8,00m de largura. De quanto aumenta a força exercida sobre a par
(Embolia gasosa em viagens de avião) Os mergulhadores são aconselhados a não viajar de avião nas primeiras 24 horas após um mergulho, porque o ar pressurizado usado durante o mergulho pode introduzir
Na Fig. 14-35, a água atinge uma altura D=35,0m atrás da face vertical de uma represa com W = 314m de largura. Determine (a} a força horizontal a que está submetida a represa por causa da pressão mano