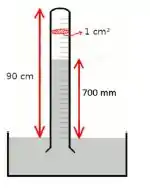
A figura mostra um tubo de vidro do barômetro de mercúrio cujo espaço acima da superfície livre do reservatório de mercúrio tem um volume de . Num dia em que a temperatura ambiente é de 20°C e a pressão atmosférica verdadeira é de 750 mmHg, a altura da coluna barométrica é de 700 mmHg. Calcule o número de mols de ar aprisionado no espaço acima da coluna de mercúrio.
Passo 1
E aí, galerinha! Tudo na paz por aí?
Meu Deus, agora tem um bololo de coisas aqui que vamos ter que ver com cuidado. Mas fica tranquilo que juntos a gente resolve qualquer parada.
Bem, o primeiro questionamente tem que vir do próprio comando da questão! Ele quer saber o número de mols e precisamos tentar ver quais equações podemos nos dar o número de mols de alguma parada.
Em geral usamos sempre duas equações pra isso:
Ou
A primeira de todas diz que o número de mols nada mais é do que a massa de uma parada dividido pela massa molar dessa parada. No nosso problema nada foi dito e muito menos foi dado a massa molar, então corre dessa alternativa pra calcular.
A segunda é vindo da lei dos gases ideias, e olha, ela depende da pressão, temperatura e volume, que de forma indireta e direta foi dada no enunciado pra gente.
Então isso nos dá um indício que o caminho é esse certo?
Então vamos seguir por aqui, beleza chuchuzinho?
Passo 2
Bem, o enunciado nos disse que temos ali uma coluna de mercúrio com uma dada pressão atmosférica verdadeira de na temperatura de 20°C. A coluna tá parada, então podemos lembrar da nossa famosa hidrostática que nos diz que a pressão em um dado ponto é igual a soma das pressões hidrostáticas que estão acima desse ponto.
Eu marquei em azul aqui o ponto que estamos analisando!
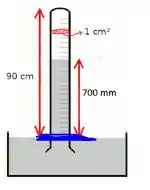
Logo, a pressão barométrica verdadeira vai ser a soma da pressão hidrostática de mercúrio acima com a coluna de ar que tem acima também, certo?
Vamos isolar essa pressão do gás?
Passo 3
Opa, a gente precisava dessa informação pra completar nosso probleminha, se lembra?
Porque precisávamos da pressão do gás. Logo, podemos substituir aqui a expressão que encontramos no passo 2.
Beleza, e quem é esse volume? É o volume que o gás ocupa dentro do tubo. Que é a área de secção transversão que equivale a multiplicada pela altura que é .
Logo:
Note que eu convertir a área de cm² para m² e a altura de cm para m.
Passo 4
O enunciado nos diz que a coluna barométrica de mercúrio é de , ou seja:
Portanto, temos que:
Esse valor equivale . Como eu fiz essa conta?
Precisamos lembrar que e fazer uma regra de três de tal forma que:
Chegamos na resposta e viu como você foi construindo comigo o raciocínio e no final arrasamos!
Te espero na próxima questão!