A figura abaixo mostra três recipientes com a mesma área da base e contendo o mesmo fluido incompressível, que exerce a mesma força F sobre a base. Considere que os recipientes têm a mesma massa.
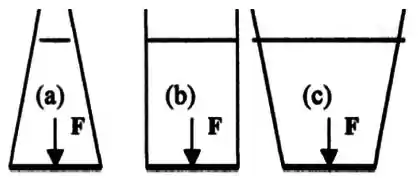
De acordo com o paradoxo hidrostático, podemos dizer que, a relação correta entre a força e o peso de fluido em cada um dos recipientes é:
Passo 1
O paradoxo hidrostático diz que, como a pressão hidrostática só depende da altura, no fundo dos recipientes as pressões serão iguais, mesmo tendo massas de fluido diferentes.
Lembrando que pressão é
Onde é força e é a área. Como os três tem a mesma área da base, a força é a mesma em todos.
Passo 2
No caso , temos que a força devido a pressão hidrostática é exatamente igual ao peso do líquido, pois como as paredes são perpendiculares ao fundo, estas não exercem peso no fundo do recipiente.
Já em , temos menos líquido, logo menos peso, do que em b, então
Em , temos mais líquido do que em , logo,
Assim,
Resposta
Letra