Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pressão Hidrostática

Ver Teoria
Exercício 231234567891011121314151617181920212224252627282930313233

Enunciado

Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 14 – Exercício 30.

(Cap 14 - Ex 30) Uma esfera de plástico oca é mantida submersa em um lago de água doce amarrada a uma corda presa no fundo do lado. O volume da esfera é igual a 0,650 m 3 , e a tensão na corda é igual a 900N. a) calculce a força de empuxo exercida pela água sobre a esfera. B) qual é a massa da esfera? c) a corda se rompe e a esfera sobe até a superfície. Quando ela atinge o equilíbrio, qual é a fração do volume da esfera que fica submersa?

Passo 1

Fala galerinha, show de bola?

O enunciado nos fornece duas informações importantes que são:

A esfera de volume , V = 0.650 m 3

Tensão, T = 900   N

Esboçando um diagrama para melhor visualização temos

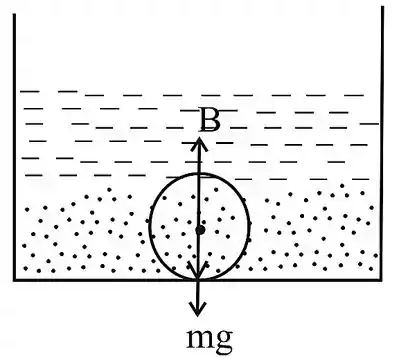
Vamos utilizar a equação do empuxo

B = ρ a g u a V o b j g

A força total na esfera é zero.

A densidade da água é de ρ = 1,00 × 10 3 k g / m 3

Passo 2

  1. Assim, aplicando a equação de empuxo, temos

    2. B = ( 1000 k g / m 3 ) ( 0,650 m 3 ) ( 9,8 m / s 2 )

    = 6370   N

    Passo 3

  2. Para que possamos calcular a massa da esfera, sabemos que

B = T + m g

Logo, substituindo na fórmula, teremos a seguinte expressão

m = B - T g

= 6,37 × 10 3 N - 900 N 9,8 m / s 2

= 558 k g

Passo 3

Agora, considerando o volume submerso “V”

B = ρ a g u a V s u b g

Onde V s u b é é o volume da esfera que está submersa.

Como

B = m g

Logo, temos que

ρ a g u a V s u b = m g

Então aplicando a teoria com os valores, teremos

V s u b = m ρ a g u a = 558 k g 1000 k g / m 3 = 0,558 m 3

Convertendo esse valor em porcentagem, temos:

V s u b V o b j = 0,558 m 3 0,650 m 3 = 0,858 = 85,5 %

Resposta

  1. 6,37 × 10 3 N
  2. 558 k g
  3. 85,5 %

Exercícios de Livros Relacionados

Em uma girafa, com a cabeça 2,0m acima do coração e o coração 2,0m acima do solo, a pressão manométrica (hidrostática) do sangue na altura do coração é 250t o r r . Suponha que a girafa está de pé e a
Alguns membros de uma tripulação tentam escapar de um submarino avariado 100m abaixo da superfície. Que força deve ser aplicada a uma escotilha, de 1,20m ×0,6m , para empurrá-la para fora a essa profu
Um grande aquário de 5 m de altura está cheio de água doce até uma altura de 2 m . Uma das paredes do aquário é feita de plástico e tem 8,00m de largura. De quanto aumenta a força exercida sobre a par
(Embolia gasosa em viagens de avião) Os mergulhadores são aconselhados a não viajar de avião nas primeiras 24 horas após um mergulho, porque o ar pressurizado usado durante o mergulho pode introduzir
Na Fig. 14-35, a água atinge uma altura D=35,0m atrás da face vertical de uma represa com W = 314m de largura. Determine (a} a força horizontal a que está submetida a represa por causa da pressão mano