O tanque fechado mostrado na figura é preenchido com água e tem de profundidade. Um manômetro, conectado a tampa do tanque, registra o valor de . Determine:
- A altura da coluna de água no tubo conectado ao tanque para que o fluido permaneça em repouso, considerando a extremidade superior do tubo aberta
- A pressão manométrica atuando no fundo do tanque
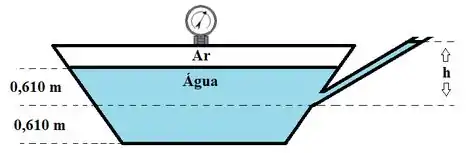
Passo 1
Falai povo bonito, como vocês estão? A figura que o enunciado nos dá está em repouso. Ou seja, o nível de água dentro desse tanque estranho não está subindo! Isso normalmente aconteceria porque a coluna de líquido dentro da conexão iria forçar sua entrada. Ela não consegue porque a pressão lá dentro impede! Se não impedisse, isso aconteceria:
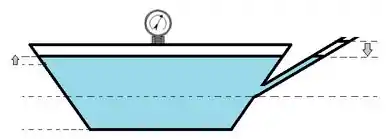
O nível de água no tanque subiria e o da conexão desceria, até a altura de líquido ser igual nos dois! Como isso não acontece, quer dizer que a pressão que o ar do lado de dentro faz é compensada pela pressão da coluna líquida acima do nível do tanque que, como está aberta pra atmosfera, ganha um reforço dela:
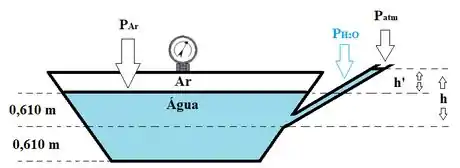
Assim, igualamos:
Como a pressão manométrica é:
Encontramos então a pressão da coluna líquida:
E como isso ajuda a gente? Bem galera, a pressão de uma coluna líquida pode sempre ser expressa como:
Onde é a altura da coluna líquida! E pelo que vemos na imagem, dá pra relacionar com mole! Vamos ter:
Sendo assim, vamos acabar ficando com:
Substituindo , constantes conhecidas, no , a altura sai em metros direto galera! Vamos ter:
Passo 2
Ta acabaaando! Agora vamos encontrar a pressão manométrica no fundo do tanque, ok? No fundo do tanque temos três coisas fazendo pressão:
- O ar dentro do tanque
- A coluna inteira de líquido
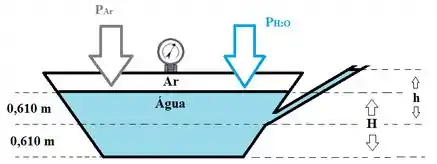
Sendo assim, temos:
Se subtrairmos os dois lados pela pressão atmosférica, olha só o que acontece:
Po galera! A definição de pressão manométrica aparece dos dois lados! E do lado direito, isso é o dado do enunciado! Vamos ter:
Calculando a pressão da coluna líquida agora e substituindo os valores::