Considere uma prensa hidráulica. Qual deve ser a relação entre os diâmetros para que a força de um lado seja igual a um quarto da força no outro lado?
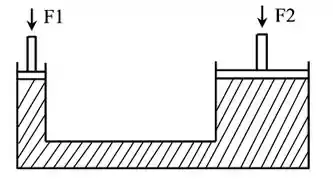
Passo 1
Como as pressões são iguais, temos que
Logo:
E isso é equivalente a:
Queremos que a relação entre as forças seja . Logo:
Substituindo na igualdade acima, encontramos as relações entre as áreas:
Passo 2
A área do círculo é dada por .
Substituindo na relação entre as áreas:
Como a razão tem que ser positiva, podemos tirar a raiz nos dois lados:
Sendo o diâmetro o dobro do raio, podemos multiplicar por em cima e embaixo:
Logo:
Resposta
Exercícios de Livros Relacionados
Um êmbolo com uma seção reta a é usado em uma prensa hidráulica para exercer uma pequena força de módulo f sobre um líquido que está em contato, através de um tubo de ligação, com um êmbolo maior de s
Um êmbolo com uma seção reta a é usado em uma prensa hidráulica para exercer uma pequena força de módulo f sobre um líquido que está em contato, através de um tubo de ligação, com um êmbolo maior de s
Um tubo em forma de U contendo um liquido possui uma seção horizontal de comprimento igual a l (Figura 14.40). Calcule a diferença de altura entre as duas colunas de liquido nos ramos verticais quando
O pistão de um elevador hidráulico de carros possui diâmetro igual a 0,30m. Qual é a pressão manométrica, em pascals, necessária para elevar um carro com massa igual a 1200 kg? Expresse essa pressão t
4. Calcule a magnitude F da força exercida por um fluido sobre uma área A de parede plana( inclinada de um ângulo qualquer em relação à vertical), do recipiente que o contém. Para isto, divida a área