Um êmbolo com uma seção reta é usado em uma prensa hidráulica para exercer uma pequena força de módulo sobre um líquido que está em contato, através de um tubo de ligação, com um êmbolo maior de seção reta .
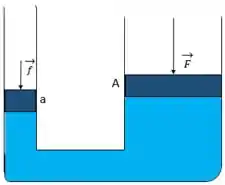
(a) Qual é o módulo da força que deve ser aplicada ao êmbolo maior para que o sistema fique em equilíbrio?
(b) Se os diâmetros dos êmbolos são e , qual é o módulo da força que deve
ser aplicada ao êmbolo menor para equilibrar uma força de aplicada ao êmbolo maior?
Passo 1
(a) Queremos para que o sistema fique em equilíbrio. Bom, pelo princípio de Pascal a gente tem que a pressão exercida no êmbolo menor é igual a exercida no êmbolo maior e a pressão é dada por:
Logo, igualando as pressões no êmbolo menor e no maior:
Isolando a força :
Passo 2
(b) Vamos usar o princípio de Pascal de novo!! Na verdade a situação dessa letra é bem parecida com a da letra (a), só que agora nós queremos a fórmula para a força no êmbolo menor e temos os valores para substituir na fórmula encontrada e fazer as contas!
Pelo princípio de Pascal, vimos que:
Agora, isolando :
Passo 3
Beleza! Agora, vamos calcular essas áreas!
Lembrando que a área das seções será dada pela área do círculo:
Como o diâmetro do êmbolo menor é , o raio será e, então, sua área .
Como o diâmetro do êmbolo maior é , o raio será e, então, sua área A.
Além disso, vamos ter que a força sobre o êmbolo maior vale .
Passo 4
Show! Dessa forma, podemos substituir os valores encontrados na fórmula que encontramos para no passo 2:
E calculando esse cara aí, chegamos que: