De quanto deve variar a pressão no tubo direito do elevador hidráulico da figura abaixo para que suba de Considere .
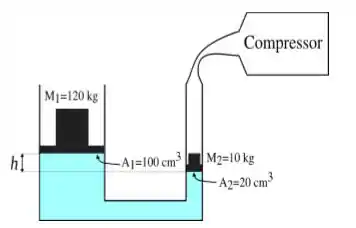
Passo 1
A água é um líquido incompressível e por isso para que suba , significa que do lado de o nível da água deve subir . Mas para que a água suba desse lado do outro a água deve descer.
O volume de água que vai para o lado de é o mesmo volume de água que sai do lado .
Temos as áreas e sabemos o quanto a altura em vai aumentar, assim conseguimos descobrir
Adotando nosso zero na posição inicial de . Nosso novo estado será:
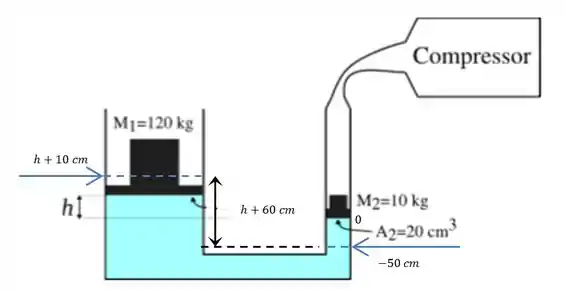
Onde a diferença de altura entre os blocos será de
Passo 2
Podemos calcular a variação da pressão pela variação da altura entre os blocos. A diferença inicial era , que correspondia a pressão causada pelos pesos, pela pressão da atmosfera e pela diferença de altura entre os pesos.
Como no caso posterior a pressão da atmosfera e os pesos continuaram os mesmo a variação da pressão irá influenciar exclusivamente na diferença de altura entre os blocos.
Pelo Principio de Stevin vimos que a pressão causada por uma coluna de líquido é
A diferença de altura no inicio era e depois passou a ser . Assim a diferença entre o estado inicial e final é
E a diferença de pressão que causou essa variação é
Resposta
Alternativa