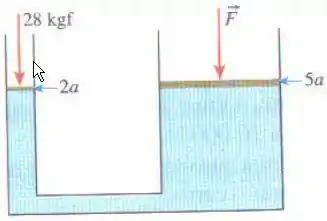
A prensa hidráulica mostrada na figura está em equilíbrio. Sabendo-se que os êmbolos possuem uma relação de áreas de , determine a intensidade da força .
Passo 1
Temos uma prensa hidráulica em equilíbrio.
Então, aplicaremos o Princípio de Pascal:
As pressões são iguais em cada extremidade:
Logo:
Passo 2
Conhecemos as relações entre as áreas nos dois lados:
No lado esquerdo, sabemos a força aplicada:
Observação: mesmo que a gente não conheça essa unidade de força, isso não influencia nas contas. No final, encontraremos nessa mesma unidade!
Passo 3
Substituindo fórmulas:
Rearranjando:
Passo 4
Substituindo valores:
Resposta
Exercícios de Livros Relacionados
Um êmbolo com uma seção reta a é usado em uma prensa hidráulica para exercer uma pequena força de módulo f sobre um líquido que está em contato, através de um tubo de ligação, com um êmbolo maior de s
Um êmbolo com uma seção reta a é usado em uma prensa hidráulica para exercer uma pequena força de módulo f sobre um líquido que está em contato, através de um tubo de ligação, com um êmbolo maior de s
Um tubo em forma de U contendo um liquido possui uma seção horizontal de comprimento igual a l (Figura 14.40). Calcule a diferença de altura entre as duas colunas de liquido nos ramos verticais quando
O pistão de um elevador hidráulico de carros possui diâmetro igual a 0,30m. Qual é a pressão manométrica, em pascals, necessária para elevar um carro com massa igual a 1200 kg? Expresse essa pressão t
4. Calcule a magnitude F da força exercida por um fluido sobre uma área A de parede plana( inclinada de um ângulo qualquer em relação à vertical), do recipiente que o contém. Para isto, divida a área