Numa prensa hidráulica, um pistão, cuja seção transversal tem área , exerce uma pequena força no líquido contido na prensa. Este líquido passa através de um tubo para outro recipiente de área , conforme a figura abaixo:
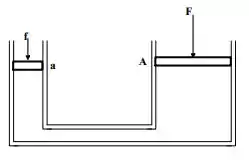
Determine a força que o pistão maior deve suportar
Se o pistão menor tiver um diâmetro de e o diâmetro do pistão maior for igual a , que peso deve ser colocado sobre o pistão menor para que o pistão maior possa suportar uma massa de toneladas?
Calcule a distância percorrida pelo pistão maior para que o pistão menor se eleve até uma altura de .
Passo 1
Bem, aqui vamos usar o famoso Princípio de Pascal! Primeiramente, devemos encontrar uma relação entre as forças atuantes em cada pistão e suas áreas. Então, vamos lá:
O Princípio de Pascal nos diz que as pressões nos dois pistões serão iguais, já que ambos estão na mesma altura. Logo:
Queremos determinar Logo, basta que manipulemos a equação acima. Assim, a força que o pistão maior deve suportar é dada pela expressão:
Passo 2
Estamos agora numa situação parecida com a , só que agora temos que achar . Vamos ver quais informações nós temos:
Massa que será colocada sobre o pistão maior: Diâmetro maior : Diâmetro menor:
Vamos primeiro calcular
Essa força nada mais é do que o peso que será posto sobre o pistão, logo, sabendo a massa e usando :
Vamos calcular agora as áreas das extremidades dos pistões, lembrando de usar a metade dos valores dos diâmetros (raios):
Logo, será:
Passo 3
O pulo do gato para resolver essa opção é levar em consideração que o volume deslocado por um pistão tem que ser o mesmo deslocado pelo o outro, já que o fluido é incompressível. Logo:
Diâmetro maior : Diâmetro menor:
Sendo e :