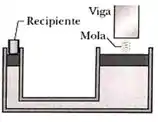
A figura mostra uma mola de constante elástica ligada a uma viga rígida e ao êmbolo de um macaco hidráulico. Um recipiente vazio de massa desprezível está colocado sobre o outro êmbolo. A relação das áreas dos êmbolos é . Com o recipiente vazio, a mola se encontra relaxada. Quantos quilogramas de areia devem ser despejados no recipiente para que a mola sofra compressão de ? ( Use na sua resposta a quantidade adequada de algarismos significativos.
Passo 1
Fala, aí!
Repara que ele diz que , então é seção maior, onde temos a mola.
Ao perguntar a quantidade de areia que deve ser colocada no recipiente, ele está nos levando a pensar com que força a gente precisa empurrar esse êmbolo onde o recipiente vai ser posicionado.
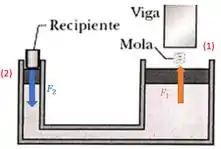
para que o êmbolo na seção seja empurrado para cima e comprima a mola, que está inicialmente relaxada, ou seja, com deformação:
para que fique com a deformação de
Então, a gente precisa achar uma relação entre e , para descobrir a massa que a gente precisa no recipiente que vai causar .
Vem comigo descobrir!
Passo 2
Já vou começar te dando um bizu: se o enunciado falar de macaco hidráulico, você pensa logo no Princípio de Pascal!
Ele diz que a pressão, quando acionada sobre um líquido em equilíbrio, vai ser transmitida para todos os pontos do líquido.
E no que isso nos ajuda? Cara, ele diz que não há pesos em cima dos êmbolos no começo da situação do enunciado, daí a gente considera que esse líquido estava em equilíbrio.
Agora vamos olhar nossa figura:
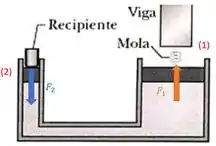
Se uma pressão for aplicada na seção do nosso macaco hidráulico, ela vai ser transmitida totalmente até a seção . O que significa que as pressões nessas seções vão ser iguais!
Passo 3
Mas lembra que a gente pode escrever a pressão numa seção pela expressão:
Então, a gente pode substituir ali
E como ele diz que:
Nossa expressão fica:
Passo 4
Beleza, achamos uma relação entre e . Agora a gente precisa colocar elas em função dos dados do nosso problema.
Temos que é a força peso do recipiente com gramas de areia exercita sobre o êmbolo, a qual podemos escrever assim:
Sendo a gravidade, que foi dada.
E é a força elástica necessária para deformar a mola . Essa força elástica tem a expressão:
Sendo a constante elástica da mola que também foi dada.
Aí a gente substitui essas expressões para as forças na nossa expressão e isola , a massa de areia que a gente quer achar:
Passo 5
Agora é substituir os valores desses dados. Mas lembra de colocar todo mundo no , para nossa massa sair em .
Prontinho!