Considere uma fibra óptica simples, retilínea, composta por um núcleo cilíndrico de índice de refração , envolvido por uma cascata cilíndrica de índice de refração .
No ponto de entrada da fibra óptica há uma fonte pontual que emite luz em todas as direções, isotropicamente. Sabemos que parte da radiação que entra na fibra é perdida para o exterior.
Suponha que todo raio luminoso que atinge a interface entre os dois meios com ângulo de incidência menor do que o ângulo limite de reflexão total seja totalmente transmitido para o exterior.
Neste caso, se a potência luminosa que entra na fibra é , podemos dizer que a potência perdida pela fibra para o exterior será:
A)
B)
C)
D)
E)
F)
Passo 1
Esse problema na verdade são dois problemas em um. Vamos primeiro tentar separar os dois, e ver qual o papel de cada um deles nessa história.
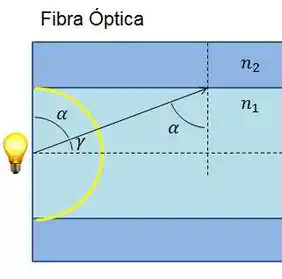
Na imagem acima, a semicircunferência amarela representa a luz que sai da fonte isotrópica. Quando uma fonte é isotrópica, ela emite luz para todas as direções, formando uma esfera luminosa ao seu redor, na qual a potência da luz vai se espalhando.
Os raios de luz incidem na interface entre as duas camadas da fibra óptica com diferentes ângulos, parte fica presa no núcleo central e parte sai desse núcleo. Isso depende do ângulo crítico entre as duas camadas.
Toda a luz que entra na camada externa da fibra óptica nós consideramos como uma potência luminosa perdida. Com isso, nossas etapas são as seguintes:
- Encontrar o ângulo crítico entre as duas camadas da fibra óptica, para saber quais raios entram e quais raios saem do seu núcleo. (Achar ângulo crítico)
- Sabendo o ângulo que os raios precisam fazer para se manter no núcleo, queremos ver a parte corresponde da esfera na qual se espalha nossa potência. (Variação da intensidade com a área)
Passo 2
Primeiro, vamos encontrar o ângulo crítico. Para isso, fazemos como se o ângulo de refração fosse igual a na lei de Snell, o que nos dá:
Temos o ângulo a partir do seno dele. (Veremos mais tarde que não precisamos do ângulo em si, e sim do seno). Agora respire fundo, descansa um pouco, e se prepara pro próximo passo que é chato.
Passo 3
Agora, vamos buscar a área correspondente à potência perdida. Pela imagem lá de cima, podemos relacionar o ângulo que cada raio faz com o centro da fibra óptica com o ângulo de incidência:
Quando aumenta, diminui, e a luz começa a ser perdida. É mais fácil calcular a área da potência não perdida, que corresponde a ou que é a calota:
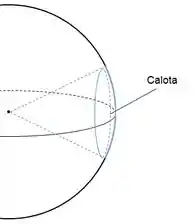
A área da calota é dada pela seguinte fórmula:
Ela pode ser encontrada integrando elementos de área de uma esfera.
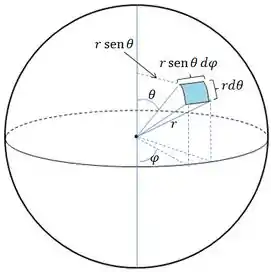
O elemento de área vai ser:
Iremos integrar de até e de até (calota no topo da circunferência).
Para traduzir pro nosso problema, giramos a calota.
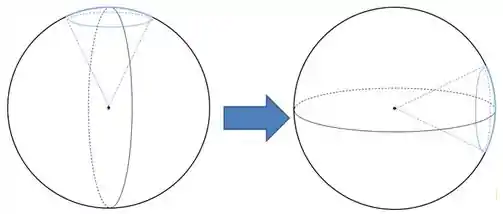
Assim, onde era , no nosso problema vira e chegamos em . Podemos traduzir direto pra , pois:
(ufa, foi muito trabalhoso isso! Vou até pedir uns 2 dias de férias no responde aí...)
Passo 4
Depois disso tudo pra achar a área, o problema volta a ser só de física (finalmente...).
A potência da luz é dada por:
Onde é a intensidade luminosa . Assim, a potência incidente total vai ser igual a:
Onde é a intensidade da luz. A potência correspondente a luz que se mantém na fibra óptica, pela nossa discussão anterior, corresponde a área da calota:
Assim, a fração da potência que se mantém na fibra ��ptica vai ser:
Considerando que toda a potência que entra ou fica na fibra ou é perdida pela saída de luz do núcleo, a fração que vai sair da fibra então vai ser:
A potência perdida é:
Obs:
A altura da calota sendo , uma outra fórmula pra área da calota é:
Que é equivalente à nossa, pois , onde é a distância do centro da circunferência até a “base” da calota.