Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Reflexão Total da Luz

Ver Teoria
Exercício 1712345678910111213141516

Enunciado

A luz passa por uma rede com 200   l i n h a s / m m e é observada em uma tela de 60   c m de largura posicionada a 1,0   m atrás da rede. Três franjas brilhantes são detectadas por um sensor foto-sensível em cada lado da franja central. Qual o valor máximo possível para o comprimento de onda da luz usada?

  1. 478   n m
  2. 733   n m
  3. 558   n m
  4. 644   n m
  5. 745   n m

Passo 1

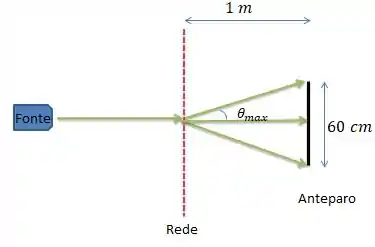
Cara, antes de sairmos com a matemática, vamos entender o problema com um desenho, pode ser?

Nós temos aqui uma rede com 200   l i n h a s / m m , e atrás dessa rede tem um anteparo de 60   c m ...

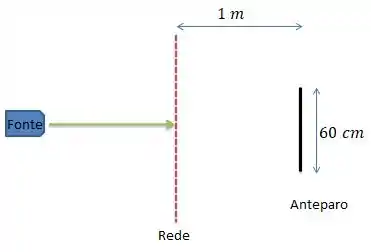
Usando uma fonte a gente incide um feixe luminoso na rede...

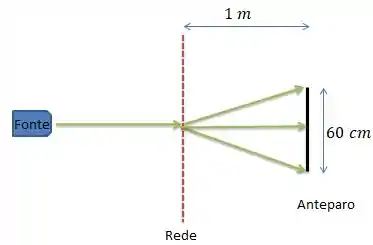
Essa luz então passa pelas fendas entre as linhas e sofre interferência gerando um padrão luminoso no anteparo com três faixas claras...

Isso significa que existe um ângulo máximo para existir essas três faixas. A esse ângulo vou dar o nome de θ m á x ...

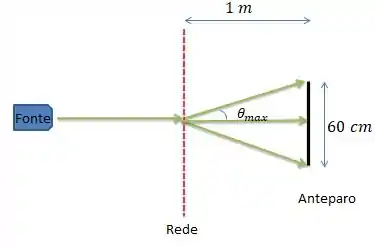
Bem, pela nossa teoria de uma rede de fendas, o ângulo máximo de existência de uma quantidade m de feixes claros está associado pela fórmula...

m   λ m á x = d   sin ⁡ θ m á x

Onde d é largura de cada fio da rede. Observe que assim, a gente pode encontrar o comprimento de onda máximo λ m á x que foi pedido no problema. Bora?

Passo 2

Repare que por trigonometria, podemos descobrir o valor de θ m á x para a existência de três franjas claras...

Ou seja...

tan ⁡ θ m á x = 60   c m / 2 1   m

Como 60   c m = 0,6   m ...

tan ⁡ θ m á x = 0,3

Ou seja...

θ m á x = arctan ⁡ 0,3 = 16,6 °

Passo 3

Também podemos descobrir o valor de d (largura de cada fio da rede). E é bem tranquilo, veja...

A rede tem...

200   l i n h a s / m m

Então, uma linha terá 1 dividido por 200   m i l i (lembre-se de que m i l i = 10 - 3 )...

d = 1 200 ⋅ 10 - 3 = 5000 ⋅ 10 - 9   m

Ou ainda...

d = 5000   n m

Onde n é de n a n o = 10 - 9 .

Passo 4

Com d e θ m á x encontrados e sabendo que temos m = 3 faixas claras no anteparo...

m   λ m á x = d   sin ⁡ θ m á x   →

  λ m á x = d sin ⁡ θ m á x m   →

Substituindo...

  λ m á x = 5000 sin ⁡ 16 ° 3   →

λ m á x = 478

Só que 478 o que? Ou seja, qual a unidade de medida?

Ora, d está em n m (nanômetros), então λ m á x também vai estar em n m ...

λ m á x = 478   n m

E esse é o valor correspondente ao máximo comprimento de onda para ter 3 faixas claras ali no anteparo.

Resposta

Letra A.

Exercícios de Livros Relacionados

Um peixe-gato está a 2 m abaixo da superfície de um lago. (a) Qual é o diâmetro da circunferência na superfície que delimita a região na qual o peixe pode ver o que existe do lado de fora do lago? (b)
Na figura 33-62, um raio luminoso incide com um ângulo θ em uma face de um cubo de plástico transparente feito de um material cijo índice de refração é 1,56. As dimensões indicadas na figura são H = 2
A figura 33-61 mostra uma fibra ótica simplificada: um núcleo de plástico n 1 = 1,58 envolvido por um revestimento de plástico com um índice de refração menos n 2 = 1,53 . Um raio luminoso incide em u
No diagrama de raios da figura 33-63 onde os ângulos não estão desenhados em escala, o raio incide com um ângulo crítico na interface dos matérias 2 e 3. O ângulo ϕ é 60° e dois dos índice de refração
Um raio de luz branca que estava se propagando no quartzo fundido incide em uma interfacequartzo-ar com um ângulo θ 1 . Suponha que o índice de refração do quartzo é n = 1,456 na extremindade vermelha