O reservatório de metal de lados e representado na figura está totalmente preenchido com um líquido desconhecido. O observador, cujo olho está nivelado com o topo do tanque, pode apenas ver o canto . O índice de refração do presente líquido vale:
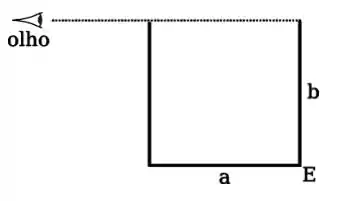
Passo 1
Este é um problema de reflexão total da luz!
O líquido no reservatório tem um índice de refração maior que o do ar, no lado de fora do reservatório.
Assim, quando a luz sai do reservatório para o ar, ela se propaga no ar fazendo um ângulo maior com a normal à superfície do que quando ela atinge a superfície pelo líquido.
Quando a luz sai do ponto E, ela segue em direção a quina esquerda da superfície, e faz um ângulo de com a normal à superfície.
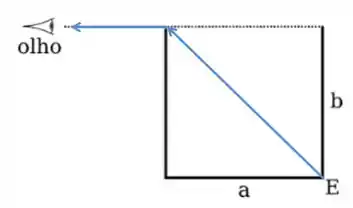
O motivo de sabermos que a luz bate ali na quina superior esquerda é que, se não fosse assim, a pessoa poderia ver outros pontos à esquerda do ponto E!
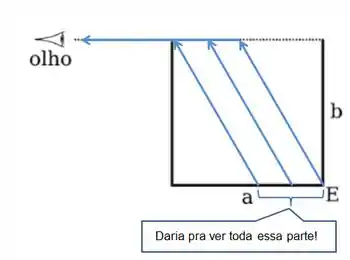
Passo 2
Pela lei de Snell Descartes, temos então:
Como fora do reservatório teria ar, temos e , o que dá .
Da construção que fizemos antes, podemos achar o seno do ângulo de incidência! Saca só o triângulo retângulo que formamos!
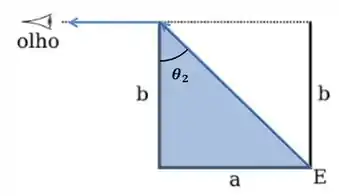
Teremos:
Onde é a hipotenusa do triângulo, que pode ser encontrada por Pitágoras:
Juntando tudo:
O que é a nossa alternativa!
Resposta
Alternativa