A luz entra em um tubo sólido feito de plástico e que possui um índice de refração igual a .
A luz desloca-se paralelamente à parte superior do tubo, conforme a figura abaixo.
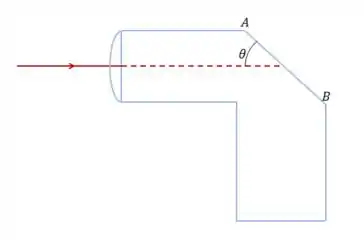
Você deseja cortar a face de modo que toda a luz seja refletida de volta para dentro do tubo depois de atingir essa face.
- Qual é o maior ângulo possível se o tubo está no ar?
- Se o tubo for imerso em água, cujo índice de refração é de , qual é o maior ângulo possível?
Passo 1
O problema nos dá o índice de refração do plástico .
O problema explica que o raio luminoso se propaga no plástico e incide sobre a superfície que separa o plástico do ar.
É importante chamar a atenção para o fato de que, quando o problema pede para calcularmos o maior ângulo possível , normalmente nós associamos ao ângulo crítico .
Porém, o ângulo pedido pelo problema não é o mesmo que o ângulo crítico .
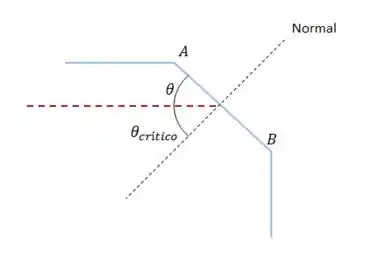
A figura acima é um zoom da região que estamos analisando.
Através da figura, vemos que, na verdade, os ângulos e estão relacionados por:
Passo 2
Letra a)
Tubo de plástico está no ar.
Podemos achar o ângulo crítico através da equação:
Onde:
;
;
Logo:
Assim:
Passo 3
Letra b)
Tubo imerso na água.
Os cálculos são os mesmos, portanto:
Onde:
;
;
Logo:
Assim:
Resposta
Letra a)
Letra b)