Um peixe-gato está abaixo da superfície de um lago.
- Qual é o diâmetro da circunferência na superfície que delimita a região na qual o peixe pode ver o que existe do lado de fora do lago?
- Se o peixe desce para uma profundidade maior, o diâmetro da circunferência aumenta, diminui ou continua o mesmo?
Considere o índice de refração da água .
Passo 1
Letra a)
O diâmetro da circunferência na superfície pedida pode ser encontrada usando o ângulo crítico da refração da luz que sai da água.
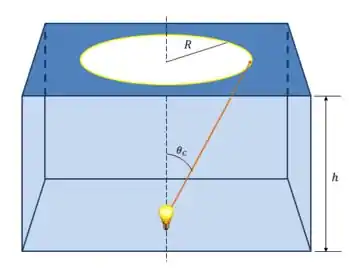
Para ângulos maiores que o crítico, a luz não sairá da água.
Pela geometria do problema, teremos:
Onde é o raio da circunferência e é a altura do peixe gato. Como o diâmetro é duas vezes o raio:
Passo 2
Agora precisamos achar o ângulo crítico.
Ele vai ser o ângulo tal que o ângulo de refração da luz no ar vai ser . Pela Lei de Snell:
Substituindo na fórmula do diâmetro, junto com a profundidade do peixe gato:
Passo 3
Letra b)
O diâmetro da circunferência é diretamente proporcional à profundidade do peixe gato.
Isso significa que quanto maior a profundidade, maior o diâmetro.
Logo, se o peixe gato descer para uma profundidade maior, o diâmetro vai aumentar.
Resposta
Letra a)
Letra b)
Se o peixe gato descer para uma profundidade maior o diâmetro vai aumentar.