Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Reflexão Total da Luz

Ver Teoria
Exercício 1412345678910111213151617

Enunciado

Reflexão e Refração

Um pequeno corpo luminoso, no fundo de uma piscina de profundidade h de água cujo índice de refração é n = 4 / 3 , emite raios para cima em todas as direções.

Uma área circular é formada na superfície da água.

Determinar o raio R do círculo de luz.

  1. 3 h / 7
  2. 4 h / 7
  3. 3 h / 5
  4. 4 h / 5
  5. 3 h / 4
  6. 4 h / 3
  7. 3   h
  8. h / 3

Passo 1

Para resolver o problema, vamos relembrar alguns detalhes.

Para conseguirmos ver o circulo luminoso, significa que todos os raios de luz provenientes do corpo luminoso que incidem sobre a área interior do círculo são refratados, passando da água para o ar.

E todos os raios que incidem na área exterior do círculo são refletidos, é por isso que não conseguimos vê-los.

A figura abaixo ilustra o que acontece.

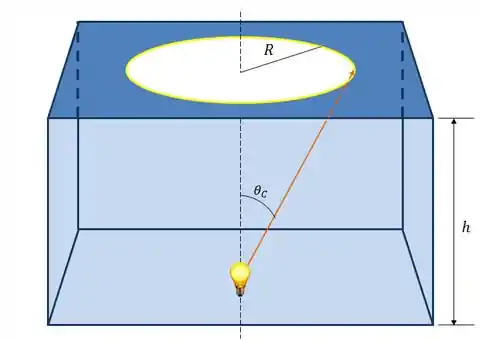
Assim, o ângulo formado pela normal à superfície da água e os raios que incidem dobre a circunferência do círculo é o ângulo crítico θ C , de forma que, para θ > θ C , todos os raios são refletidos.

O ângulo crítico é dado por

sen ⁡ θ C = n a r n á g u a

Onde:

n a r = 1 ;

n á g u a = 4 / 3 ;

Logo:

sen ⁡ θ C = 1 4 / 3 = 3 4

Agora, analisando novamente a figura, podemos escrever a seguinte relação:

sen ⁡ θ C = R R 2 + h 2

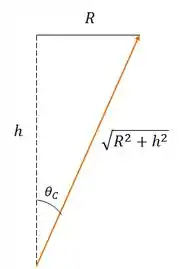
Portanto:

R R 2 + h 2 = 3 4

R 2 R 2 + h 2 = 9 16

R 2 = 9 16 R 2 + h 2 = 9 16 R 2 + 9 16 h 2

R 2 1 - 9 16 = 9 16 h 2

7 16 R 2 = 9 16 h 2

R 2 = 9 7 h 2

R = 3 h 7

Resposta

Letra (a): R = 3 h / 7

Exercícios de Livros Relacionados

Um peixe-gato está a 2 m abaixo da superfície de um lago. (a) Qual é o diâmetro da circunferência na superfície que delimita a região na qual o peixe pode ver o que existe do lado de fora do lago? (b)
Na figura 33-62, um raio luminoso incide com um ângulo θ em uma face de um cubo de plástico transparente feito de um material cijo índice de refração é 1,56. As dimensões indicadas na figura são H = 2
A figura 33-61 mostra uma fibra ótica simplificada: um núcleo de plástico n 1 = 1,58 envolvido por um revestimento de plástico com um índice de refração menos n 2 = 1,53 . Um raio luminoso incide em u
No diagrama de raios da figura 33-63 onde os ângulos não estão desenhados em escala, o raio incide com um ângulo crítico na interface dos matérias 2 e 3. O ângulo ϕ é 60° e dois dos índice de refração
Um raio de luz branca que estava se propagando no quartzo fundido incide em uma interfacequartzo-ar com um ângulo θ 1 . Suponha que o índice de refração do quartzo é n = 1,456 na extremindade vermelha