Um feixe de luz propagando-se no ar () incide em uma face horizontal de um paralelepípedo, fazendo um ângulo com a normal, conforme indica a figura abaixo.
Sendo o índice de refração do paralelepípedo , para quais valores de o feixe sofrerá reflexão total na face vertical?
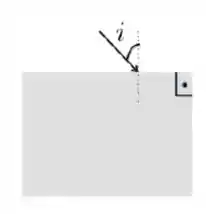
- Nunca haverá reflexão total
Passo 1
Ao se deparar com um problema novo, devemos sempre tentar entende-lo. Como ele pensa? Do que se alimenta? Onde vive? Ok, perdi o ponto aqui.
Primeiro, vamos observar a geometria do problema. Um raio luminoso incide na face superior do paralelepípedo com ângulo de incidência . Ele então sofre um desvio (ângulo de refração ) e incide na face lateral com um certo ângulo . Se for muito grande, haverá reflexão total. Caso contrário, não haverá.
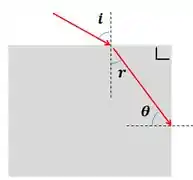
Passo 2
Podemos relacionar e pois eles são os ângulos de um triângulo retângulo (dado pelo raio dentro do paralelepípedo e as normais de ambas as faces), e logo:
Sendo que nós podemos encontrar pela lei de snell a partir do ângulo de incidência.
Além disso, o ângulo limite para que o raio sofra reflexão total na face lateral é:
Passo 3
Da discussão anterior, temos que:
Podemos inverter essa equação usando a função inversa do seno, chamada “arcoseno”.
Para achar o ângulo incidente limite, substituímos o limite. Porém, só temos o seu seno. Vamos ter que tentar achar seu coseno.
Substituindo o índice de refração do paralelepípedo , teremos:
Assim, o ângulo incidente fica:
Que é o ângulo limite.
Passo 4
Ainda não temos nossa resposta, pois para esse ângulo limite temos 2 opções: letra d) e letra c).
Para saber quais das duas estão certas, voltamos para a figura que relaciona todos os ângulos.
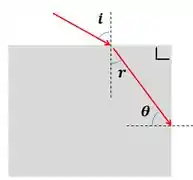
Nela, veja o seguinte: Quando eu aumento o ângulo , eu aumento o ângulo . Mas isso faz com que eu diminua o ângulo .
Ângulos menores que o limite não causam reflexão total.
Porém, se eu diminuir o ângulo , eu acabo aumentando . Logo, ângulos MENORES que o ângulo limite também vão causar reflexão total.
A resposta certa então é a letra d).
Resposta
Letra d)