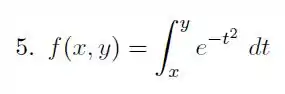
Passo 1
Vamos começar fazendo a derivada em relação a , como temos uma integral vamos usar o teorema fundamental do cálculo, mas antes precisamos deixar essa integral um pouco diferente, porque a integral nós fazermos de um número até uma função, então vamos começar arrumando isso
Passo 2
Vamos agora para a derivada, usando o teorema fundamental do cálculo e a regra da cadeia vamos ter
Passo 3
Vamos agora para a derivada em relação a , usando o teorema fundamental do cálculo e a regra da cadeia
Resposta
Exercícios de Livros Relacionados
Se f é homogênea de grau n , mostre que f x t x , t y = t n - 1 f x ( x , y )
Suponha que a equação F x , y , z = 0 defina implicitamente cada uma das três variáveis x ,y e z como função das outras duas: z = f ( x , y ) , y = g ( x , z ) e x = h y , z . Se F for diferenciável e
Se f é homogênea de grau n , mostre que x 2 ∂ 2 f ∂ x 2 + 2 x y ∂ 2 f ∂ x ∂ y + y 2 ∂ 2 f ∂ y 2 = n ( n - 1 ) f ( x , y )
Utilize a equação 6 para determinar d y // d x .cos ( x y ) = 1 + s e n y
Uma função f é dita homogênea de grau n se satisfaz a equação f t x , t y = t n f ( x , y ) para todo valor de t , onde n é o número inteiro e positivo e f tem as segundas derivadas parciais contínuas