Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra da Cadeia – Tópicos Adicionais

Ver Teoria
Exercício 1212345678910111314

Enunciado

Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 14 – Seção 5 – Exercício 43

Um lado de um triângulo está aumentando a uma taxa de 3   c m / s e um segundo lado está decrescendo a uma taxa de 2   c m / s . Se a área do triângulo permanece constante, a que taxa varia o ângulo entre os lados quando o primeiro lado tem 20   c m de comprimento, o segundo lado tem   30   c m de comprimento e o ângulo é π / 6 ?

Passo 1

Faaaala pessoal! Nesse problema, temos um triângulo como esse:

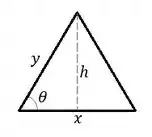
E aí um dos lados cresce 3   c m / s enquanto o outro decresce 2   c m / s . Aí queremos saber a que taxa o ângulo θ está variando quando o primeiro lado tem 20   c m , o segundo tem 30   c m e o ângulo vale π 6 , vamos lá trabalhar com taxas de variação?

Passo 2

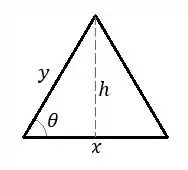
A área de um triângulo é dada por:

A = 1 2 x h

Por trigonometria, enxergando um triângulo retângulo, temos que:

sen ⁡ θ = C O h i p = h y

h = y sen ⁡ θ

Então a área do triângulo é

A = 1 2 x y sen ⁡ θ

Passo 3

Bom, a gente sabe que os lados estão variando com o tempo. Mas ao mesmo tempo, ele diz que a área não está mudando, ou seja: não está variando. Então:

d A d t = 0

Podemos calcular d A / d t pela regra da cadeia na equação da área

A = 1 2 x y sen ⁡ θ

d A d t = ∂ A ∂ x d x d t + ∂ A ∂ y d y d t + ∂ A ∂ θ d θ d t

Como d A d t = 0 :

∂ A ∂ x d x d t + ∂ A ∂ y d y d t + ∂ A ∂ θ d θ d t = 0

Substituindo as derivadas parciais da área em relação a x , y e θ :

1 2 y sen ⁡ θ d x d t + 1 2 x sen ⁡ θ d y d t + 1 2 x y cos ⁡ θ d θ d t = 0

Multiplicando a equação por 2

y sen ⁡ θ d x d t + x sen ⁡ θ d y d t + x y cos ⁡ θ d θ d t = 0

Isolando d θ / d t

d θ d t = - y sen ⁡ θ d x d t + x sen ⁡ θ d y d t

d θ d t = - y sen ⁡ θ d x d t + x sen ⁡ θ d y d t x y cos ⁡ θ

Podemos colocar sen ⁡ θ em evidencia

d θ d t = - y d x d t + x d y d t sen ⁡ θ x y cos ⁡ θ

Como s e n θ cos ⁡ θ = t g ⁡ ( θ ) :

d θ d t = - y d x d t + x d y d t x y tg ⁡ θ

Showw, agora é só substituir os valores

Passo 4

Substituindo os valores, quando x = 20 , y = 30 e θ = π / 6 , e temos também que as taxas d x d t = 3 e d y d t = - 2

d θ d t = - 30 ( 3 ) + 20 ( - 2 ) ( 20 ) ( 30 ) tg ⁡ π 6

d θ d t = - 90 - 40 600 3 3

Então:

d θ d t = - 3 36 ≈ - 0,05 r a d s

E fimmm

Resposta

d θ d t ≈ - 0,05 r a d s  

Exercícios de Livros Relacionados

Se f é homogênea de grau n , mostre que f x t x , t y = t n - 1 f x ( x , y )
Suponha que a equação F x , y , z = 0 defina implicitamente cada uma das três variáveis x ,y e z como função das outras duas: z = f ( x , y ) , y = g ( x , z ) e x = h y , z . Se F for diferenciável e
Se f é homogênea de grau n , mostre que x 2 ∂ 2 f ∂ x 2 + 2 x y ∂ 2 f ∂ x ∂ y + y 2 ∂ 2 f ∂ y 2 = n ( n - 1 ) f ( x , y )
Utilize a equação 6 para determinar d y // d x .cos ( x y ) = 1 + s e n y
Uma função f é dita homogênea de grau n se satisfaz a equação f t x , t y = t n f ( x , y ) para todo valor de t , onde n é o número inteiro e positivo e f tem as segundas derivadas parciais contínuas