UFES – Cálculo 1 – Lista 10 – Questão 20
Deduza as fórmulas
Passo 1
E aí pessoal, tudo bem? O problema nos deu essa afirmação aqui
E pediu para deduzirmos!
Mas como fazer isso?
Temos uma equação que resulta em , então a primeira coisa a se fazer é jogar aquele arco cosseno para o outro lado!
Então a ideia aqui é a seguinte: lembrar de como deduzimos as funções arcos, com aquele nosso querido triângulo, e fazer essa relação!
Lembrando que em termos de catetos opostos, adjacentes e hipotenusas, as funções cosseno e secante são
Só com isso vamos provar que aquela fórmula lá! Belezinha?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Temos
Isso é a mesma coisa que
E, se chamarmos de , vamos ter que
Assim
Tranquilo até aqui?
Passo 3
Isolando o cosseno,
Substituindo isso no lado direito da nossa equação, ficamos com
Agora, qual é o arco cujo cosseno é cosseno de ?
É o próprio , né?
Então
Passo 4
Então, no passo 1 dissemos que
E no passo 2 achamos que
Substituindo tudo isso na equação que quermos provar
Provamos que
Fim de papo! Outra forma de você ver isso é usando aquele triângulo! Lembrando que
Usando que , podemos formar um triângulo retângulo:
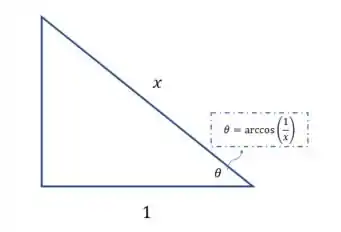e com ele podemos escrever a secante desse ângulo!
E fazendo a função inversa para isolar
E quem é esse ? É nosso Então provamos de outra forma a mesma fórmula!
Beleza? É isso! Espero ter ajudado!