UFES, Sem Campus, Cálculo 1, Listas de Estudos UFES - Cálculo 1 - Lista 11, Questão 3
Nos exercícios a esboce o gráfico da função.
Passo 1
Eaew, tudo certinho contigo?
Temos a seguinte função
queremos esboçar o seu gráfico! Então iremos ter que analisar diversas características! Como, intervalos de crescimento, decrescimento, máximos, mínimos, domínio, quando a função se anula, assim por diante! Vamos ao longo dos passos avaliar tudo que é possível! Vem comigo!
Passo 2
Primeiro, temos alguma limitação sobre o domínio da função? Ela é um logaritmo, portanto, não podemos ter números negativos dentro da função! Mas note que no argumento do logaritmo temos
portanto, esse número nunca será negativo! Mas ainda assim, teremos problemas quando esse argumento for nulo, já que não existe logaritmo de zero! Isso ocorre quando
Temos então que o domínio de nossa função é
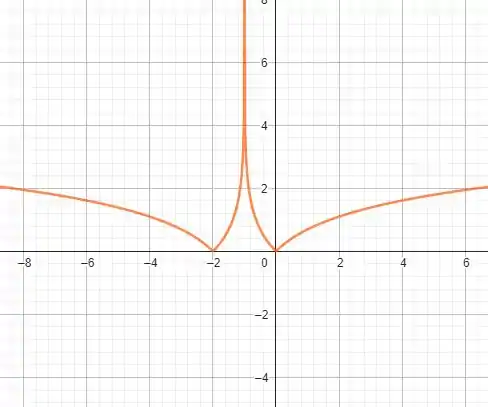
Vamos tentar analisar agora o comportamento da função nos arredores de !
Passo 3
Primeiro, note que quando o argumento do logaritmo for
temos que a função se anula! Isso ocorre para que valores? Para e , quando estivermos dentro do intervalo
e
note que é quando o logaritmo se anula e portanto estamos contando a partir deste valor. Neste pequeno intervalo, o módulo do argumento é menor do que , e portanto, a função seria negativa! Já que poríamos garantir que o seguinte limite é verdade
já que quanto mais perto de mais negativo é o nosso valor, maior em módulo, mas nunca bem definido, é uma assíntota vertical! No entanto, como estamos tomando o módulo da função como um todo, a função no intervalo
é espelhada em relação ao eixo , ou seja, o nosso limite na verdade é
E, para valores tais que e , temos o comportamento comum do logaritmo, mas espelhado em relação a , o gráfico portanto, é da forma
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!