UFES – Cálculo 1 – Lista 10 – Questão 21
Deduza as fórmulas
Passo 1
E aí pessoal, tudo bem? O problema nos deu essa afirmação aqui
E pediu para deduzir essa fórmula!
E agora, como fazer isso?
Esse é o exemplo perfeito para exercitarmos a derivada de uma função trigonométrica, usar o teorema da função inversa e de quebra ainda usar as relações de triângulo retângulo! Tudo junto!
Vamos relembrar algumas coisas?
A derivada da tangente:
O teorema da função inversa:
E das relações trigonométricas! Em relação a catetos oposto e adjacente e hipotenusa, temos que a secante (já que ela aparece na derivada da tangente) é
Beleza? Agora é juntar todas essas informações!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Precisamos provar o seguinte
Temos que derivar a função inversa da tangente, então aqui vamos usar o teorema da função inversa
Beleza? Mas já sabemos quem é a derivada da tangente!
Então, passando :
Beleza? Guarda isso!
Passo 3
Agora vamos lá no triângulo para ver quem é quem! No triângulo retângulo
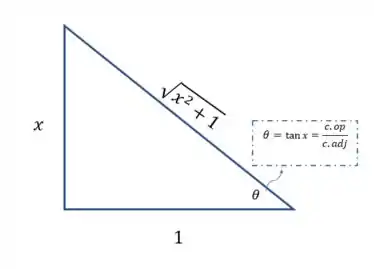
E pelo teorema de Pitágoras
então
Passo 4
Agora vamos retornar ao passo !
Lembrando que
E usando os valores de e do passo anterior temos o seguinte
Assim
E jogando isso na derivada do arco tangente
E é isso! Fórmula demonstrada!
Espero ter ajudado! Vamos para a próxima?