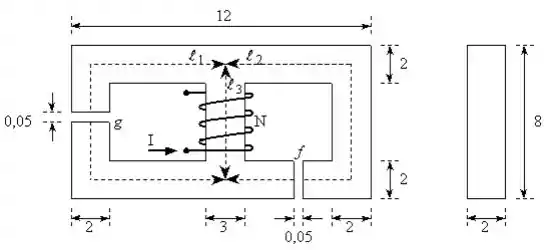
No circuito magnético abaixo, construído com uma liga de ferro-níquel, calcular a para que o fluxo no entreferro g seja de . Desprezar o espraiamento de fluxo no entreferro.
Dimensões em centímetros.
Passo 1
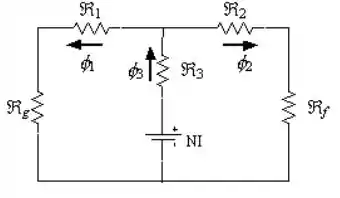
Vamos começar com o circuito elétrico análogo:
Passo 2
Em seguida, vamos separar os dados e começar a análise
Dados:
Aqui, a gente pode perceber a existência de simetria entre seus braços direito e esquerdo. Portanto,
Com isso, chegamos no seguinte conjunto de equações:
Passo 3
Para o cálculo de temos:
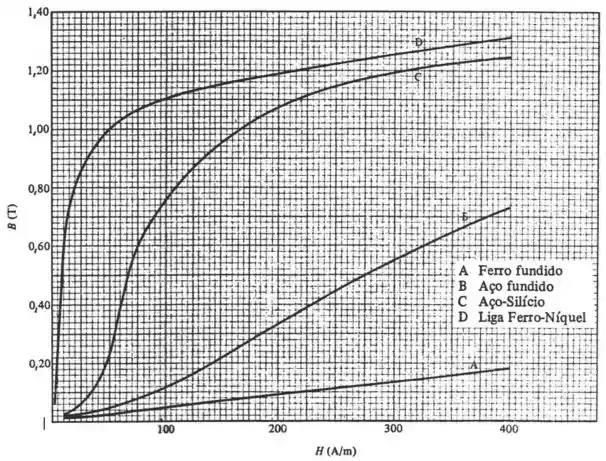
Consultando a curva de magnetização do ferro-níquel abaixo:
Para o cálculo de temos:
Para o cálculo de temos:
Como,
Novamente vamos consultar a curva de magnetização do ferro-níquel e chegamos em:
Passo 4
Substituindo todos esses valores encontrados na equação do passo 2, temos a força magnetomotriz (: