Um núcleo com três pernas é mostrado na figura abaixo:
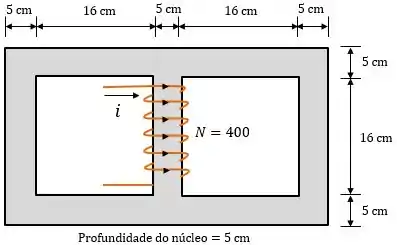
Sua profundidade é e há espiras na perna central. As demais dimensões estão mostradas na figura. O núcleo é composto de um aço cuja curva de magnetização está mostrada abaixo:
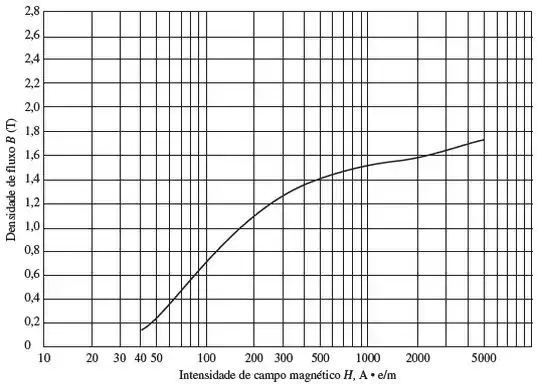
Responda às seguintes perguntas sobre esse núcleo:
Que corrente é necessária para produzir uma densidade de fluxo de na perna central do núcleo?
Que corrente é necessária para produzir uma densidade de fluxo de na perna central do núcleo? Essa corrente é o dobro da corrente da parte ?
Quais são as relutâncias das pernas central e direita do núcleo para as condições da parte ?
Quais são as relutâncias das pernas central e direita do núcleo para as condições da parte ?
Passo 1
Nesse exemplo temos três relutâncias: uma referente à perna central, uma referente ao lado esquerdo e outra referente ao lado direito.
Além disso, o fluxo produzido na perna central se dividirá em dois: um seguindo para a esquerda e outro para a direita. Logo, o circuito é paralelo e, consequentemente, as relutâncias estão associadas em paralelo.
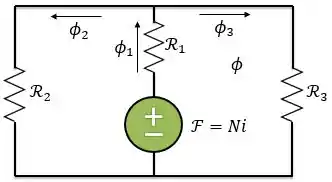
Como o fluxo é o análogo à corrente em um circuito elétrico, temos:
Passo 2
Na letra , a densidade de fluxo na perna central é . Para essa densidade de fluxo o fluxo é:
A área da seção reta é a mesma para todo o núcleo:
Logo, o fluxo na perna central será:
Passo 3
Como o núcleo é simétrico, o fluxo gerado na perna central se divide igualmente entre a perna da esquerda e da direita.
Então,
Para esses fluxos, a densidade de fluxo será:
Passo 4
Utilizando a curva de magnetização, vemos que para uma densidade de fluxo de a intensidade de campo magnético é e para uma densidade de a intensidade é .
Agora vamos calcular as permeabilidades relativas para depois calcularmos as relutâncias:
Então, vamos começar. Para a perna central, temos:
Já para as pernas laterais:
Passo 5
Como a área da seção reta é a mesma para todo o núcleo, falta calcularmos o comprimento médio relacionado à cada relutância.
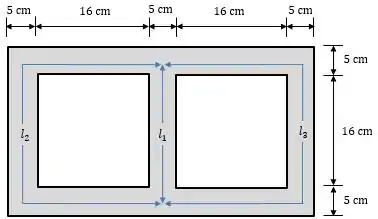
Onde:
Então, substituindo todos os valores que encontramos, temos as seguintes relutâncias:
Passo 6
Para encontrarmos a corrente, primeiro, temos que calcularmos a . Então, vamos usar o circuito magnético e a nossa relação análoga a lei de Ohm para circuitos magnéticos:
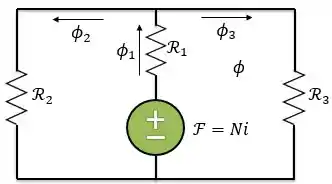
Como as relutâncias e estão em paralelo, a relutância equivalente será:
Então, substituindo os valores que calculamos:
Como
A corrente será
Passo 7
Na letra , a densidade de fluxo na perna central é . Para essa densidade de fluxo o fluxo é:
A área da seção reta é a mesma para todo o núcleo:
Logo, o fluxo na perna central será:
Passo 8
Como o núcleo é simétrico, o fluxo gerado na perna central se divide igualmente entre a perna da esquerda e da direita. Então,
Para esses fluxos, a densidade de fluxo será:
Passo 9
Utilizando a curva de magnetização, vemos que para uma densidade de fluxo de a intensidade de campo magnético é e para uma densidade de a intensidade é .
Agora vamos calcular as permeabilidades relativas. Para a perna central, temos:
Já para as pernas laterais:
Passo 10
Então, substituindo todos os valores que encontramos, temos as seguintes relutâncias:
Passo 11
Para encontrarmos a corrente, primeiro, temos que calcularmos a . Então, vamos usar o circuito magnético e a nossa relação análoga a lei de Ohm para circuitos magnéticos:
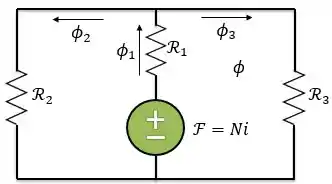
Como as relutâncias e estão em paralelo, a relutância equivalente será:
Então, substituindo os valores que calculamos:
Como
A corrente será
Passo 12
Na letra é pedido as relutâncias da perna central e direita para as condições da letra . Nós já calculamos essas relutâncias quando estávamos querendo descobrir a correnta na letra . Elas são:
Passo 13
Para terminar, na letra as relutâncias pedidas são para as condições da letra , que também já tínhamos calculado: