Dois circuitos condutores são constituídos por um fio reto bastante longo e uma espira retangular de dimensões e . A espira pertence a um plano que passa pelo fio, sendo os lados de comprimento paralelos ao fio e distantes de e deste. Determinar a expressão que fornece a indutância mútua entre os dois circuitos.
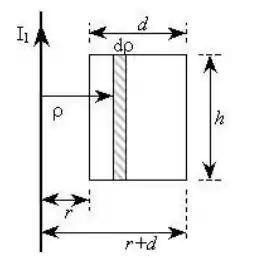
Passo 1
Vamos começar já colocando a nossa fórmula de indutância mútua aqui pra sabermos o que precisamos calcular:
Então, precisamos calcular :
Bom, sabemos que para um fio infinito de corrente temos:
então,
Agora, pra calcular o faremos a integral dessa campo magnético que achamos, ok?
Passo 2
Substituindo esse valor que encontramos lá na primeira equação, temos: