Dado o circuito magnético da figura abaixo, assumir através da seção reta da perna esquerda e determinar a queda de potencial magnético no ar .
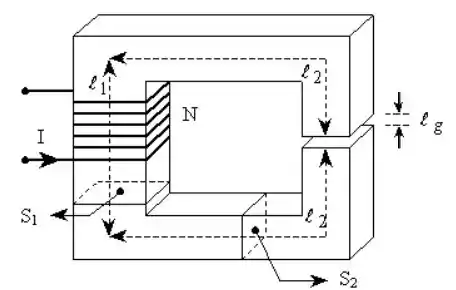
Dados:
Passo 1
Vamos começar desenhando nosso circuito elétrico análogo:
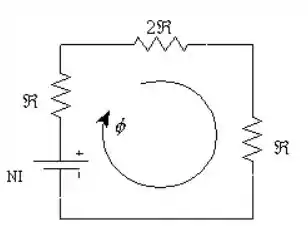
Passo 2
Pronto, agora fica bem mais fácil né?
Vamos separar nossos dados aqui e começar as contas:
Analisando o circuito chegamos na seguinte equação:
onde, é o e é o
Passo 3
Agora, basta calcularmos