Um núcleo magnético de duas pernas e um entreferro está mostrado abaixo:
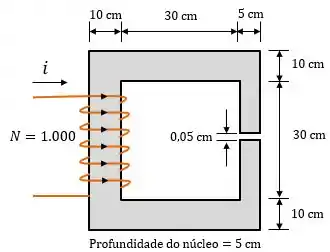
A profundidade do núcleo é , o comprimento do entreferro do núcleo é e o número de espiras no núcleo é . A curva de magnetização do material do núcleo está mostrada na abaixo:
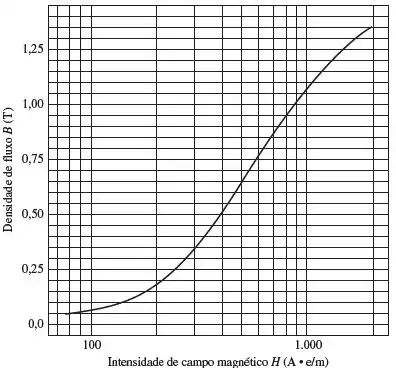
Assuma um incremento de na área efetiva do entreferro para compensar o espraiamento. Quanta corrente é necessária para produzir uma densidade de fluxo no entreferro de ? Quais são as densidades de fluxo dos quatro lados no núcleo com essa corrente? Qual é o fluxo total presente no entreferro?
Passo 1
Nesse núcleo, o fluxo é o mesmo para todas as pernas, ele só tem um caminho para circular. Então seu circuito magnético será com as relutâncias associadas em série.
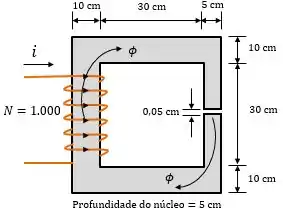
Agora, vamos analisar quantas relutâncias diferentes temos. Podemos dividir esse núcleo em três relutâncias: uma para as pernas de maior largura , uma para a perna mais estreita , e uma outra para o entreferro . Então, nosso circuito magnético será assim:
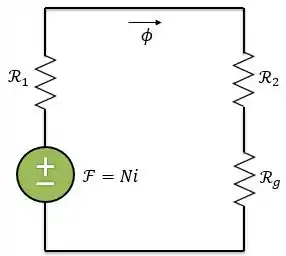
Onde:
Passo 2
Agora, vamos determinar os comprimentos médios referentes à cada relutância e as áreas das seções retas. Para ficar mais fácil vamos analisar a figura abaixo.
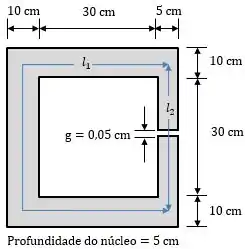
Lembrando que o comprimento tem que estar em metros, temos:
Cuidado com o comprimento ! A gente tem que descontar o comprimento do entreferro.
O comprimento do entreferro o enunciado já deu de bandeja:
Passo 3
Com os comprimentos calculador, vamos partir para o cálculo das áreas. Como a profundidade do núcleo é
Cuidado agora!!! O enunciado disse para assumir um incremento de na área efetiva do entreferro para compensar o espraiamento. O que isso quer dizer?
Na prática é simples: temos que considerar que a área da seção reta do entreferro é maior do que a área da seção reta real em que ele se encontra:

Calma que eu te explico! Vamos dar um zoom no entreferro desse núcleo:
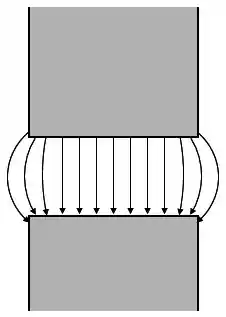
Esse é o efeito de espraiamento de um campo magnético no entreferro. Viu o aumento da área da seção reta do entreferro em comparação com a área da seção reta do metal? Por isso o enunciado pediu para a gente considerar esse efeito.
Passo 4
Agora que já sabemos a área da seção reta do entreferro, podemos calcular o fluxo. Como vimos, ele é o mesmo em todas as pernas do núcleo. Então, como o enunciado disse que no entreferro a densidade de fluxo tem que ser de , usando a equação abaixo, temos:
Pronto! Uma pergunta do enunciado já foi respondida.
Passo 5
Agora que já temos o fluxo, podemos calcular a densidade de fluxo em cada região. A primeira região é a aquela com as pernas de mesma largura, que têm comprimento médio e área da seção reta . Nela a densidade de fluxo será:
Logo, as densidades de fluxo das pernas inferior, superior e esquerda será:
Já a outra região é aquela com a perna mais fina, que tem comprimento e área . Então:
Logo a densidade de fluxo da perna da direita do núcleo é:
Passo 6
Sabemos que a permeabilidade magnética do entreferro é:
Falta determinarmos a permeabilidade magnética do núcleo, vamos fazer isso utilizando a curva de magnetização que o enunciado nos forneceu.
Também sabemos que a permeabilidade relaciona a intensidade de campo magnético e a densidade de fluxo magnético .
Logo, podemos calculá-la assim:
Cada região terá uma permeabilidade diferente, já que a densidade de fluxo é diferente em cada região.
Então, olhando no gráfico, temos:
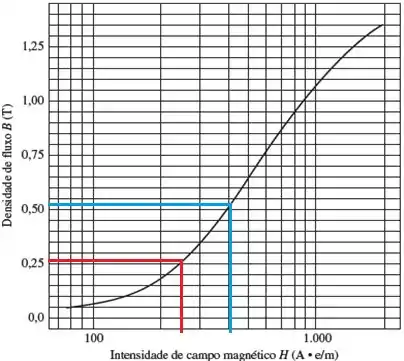
Para :
Para :
Logo, as permeabilidades magnéticas serão:
Passo 7
Finalmente temos todos os valores para calcular as relutâncias:
Passo 8
Para encontrarmos a corrente, primeiro, temos que calcularmos a . Então, vamos usar o circuito magnético e a nossa relação análoga a lei de Ohm para circuitos magnéticos:
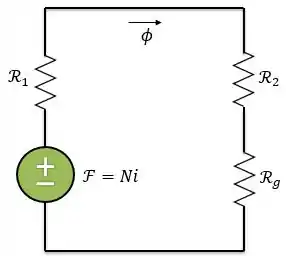
Como as relutâncias estão associadas em série, a relutância equivalente será:
Então, substituindo os valores que calculamos:
Como
A corrente será