A figura abaixo mostra o núcleo de um motor CC simples:
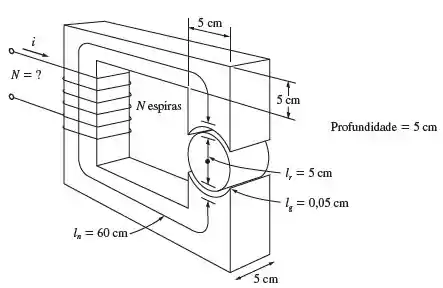
Assuma que a área da seção reta de cada entreferro seja , que a largura de cada entreferro é e que a permeabilidade relativa do núcleo é . O diâmetro efetivo do núcleo do rotor é e a densidade de fluxo no núcleo é .
Qual seria o fluxo total no núcleo para essa densidade de fluxo da parte?
A corrente de campo máxima possível para essa máquina é . Determine um número razoável de espiras de fio para fornecer a densidade de fluxo desejada e ao mesmo tempo não exceder a corrente máxima disponível.
Passo 1
Na letra , vamos calcular o fluxo no núcleo utilizando a fórmula abaixo:
Como a profundidade do núcleo é área da seção reta será:
Então, o fluxo é:
Passo 2
Na letra , vamos encontrar o número de espiras utilizando circuito magnético referente a esse núcleo. A gente vai ter quatro relutâncias associadas em série: uma referente às pernas do núcleo, uma referente ao núcleo do rotor e mais duas referente aos entreferros, que serão iguais.
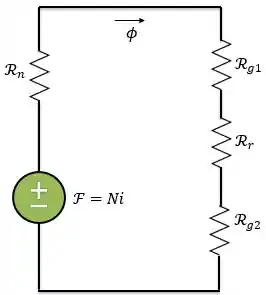
Passo 3
Agora vamos partir para os cálculos das relutâncias, lembrando que tudo tem que estar em metros:
Passo 4
Como o fluxo é o mesmo para todo o núcleo, as relutâncias estão em série e a relutância equivalente será:
Passo 5
Para encontrarmos o número de espiras, primeiro, temos que calcularmos a . Então, utilizando a relação análoga a lei de Ohm para circuitos magnéticos:
Então, substituindo os valores que calculamos:
Como
O número de espiras será:
Logo, um número razoável de espiras para atender nossas condições seria