Um núcleo ferromagnético com uma permeabilidade relativa de está mostrado na figura abaixo. As dimensões são mostradas no diagrama e a profundidade do núcleo é de . Os entreferros nos lados direito e esquerdo do núcleo são e , respectivamente. Devido ao efeito de espraiamento, a área efetiva dos entreferros é de maior do que o seu tamanho físico. Se na bobina houver espiras enroladas em torno da perna central do núcleo e se a corrente na bobina for , quais serão os valores de fluxo para as pernas esquerda, central e direita do núcleo? Qual é a densidade de fluxo em cada entreferro?
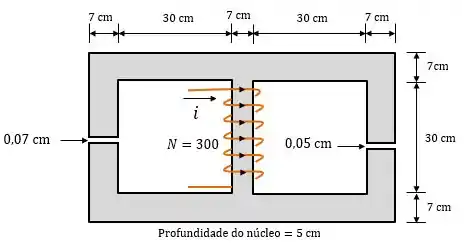
Passo 1
Vamos começar calculando os comprimentos de cada braço:
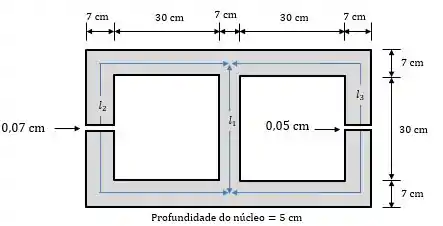
Para e temos que lembrar de subtrair o valor do comprimento dos gaps:
Passo 2
Calculando as áreas:
Passo 3
Cuidado agora!!! O enunciado disse para assumir um incremento de na área efetiva do entreferro para compensar o espraiamento. O que isso quer dizer?
Na prática é simples: temos que considerar que a área da seção reta do entreferro é maior do que a área da seção reta real em que ele se encontra:

Calma que eu te explico! Vamos dar um zoom nos entreferros desse núcleo:
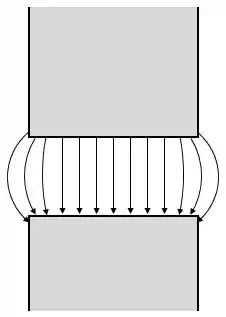
Esse é o efeito de espraiamento de um campo magnético no entreferro. Viu o aumento da área da seção reta do entreferro em comparação com a área da seção reta do metal? Por isso o enunciado pediu para a gente considerar esse efeito.
Passo 4
O circuito terá as relutâncias do núcleo e também as relutâncias associadas aos entreferros, denominadas de e O circuito do problema fica assim:
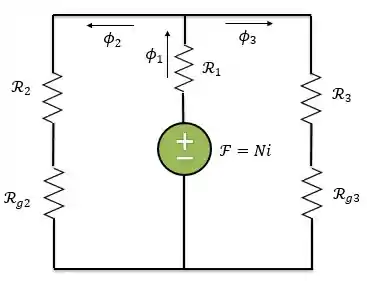
Calculando as relutâncias:
Para o cálculo das relutâncias nos entreferros, temos que lembrar que o não entra na fórmula, porque é um entreferro de ar:
Passo 5
A relutância total será:
Passo 6
Agora podemos calcular o valor do fluxo total:
Passo 7
Agora vamos calcular os fluxos da esquerda e da direita utilizando o mesmo princípio de divisor de corrente em circuitos elétricos. O fluxo da esquerda será:
Passo 8
O fluxo da direita será: