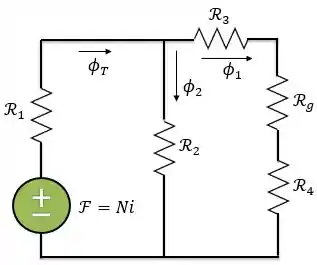
No circuito magnético apresentado abaixo, o fluxo magnético no entreferro é de . Utilizando a curva de histerese do material, determine:
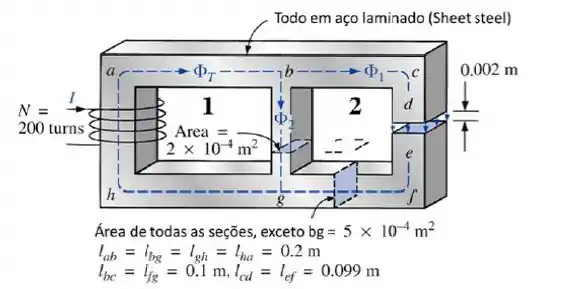
O circuito elétrico equivalente ao circuito magnético apresentado
Os fluxos indicados na figura
O valor da corrente na bobina
Passo 1
Para esse núcleo, teremos cinco relutâncias:
referente ao comprimento
referente ao comprimento (perna central)
referente ao comprimento
referente ao entreferro
referente ao comprimento
Como o fluxo gerado pelas espiras na perna da esquerda se divide entre os fluxos e , temos o circuito magnético abaixo:
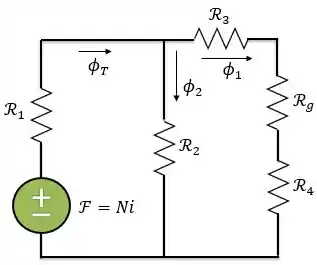
Onde:
Passo 2
O enunciado disse que o fluxo no entreferro é , ou seja:
Logo, a densidade de fluxo no entreferro e em todo lado direito será:
Como a área da seção reta é para todo o núcleo, exceto no entreferro, temos:
Passo 3
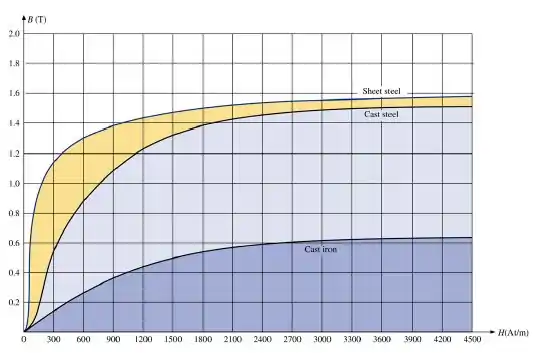
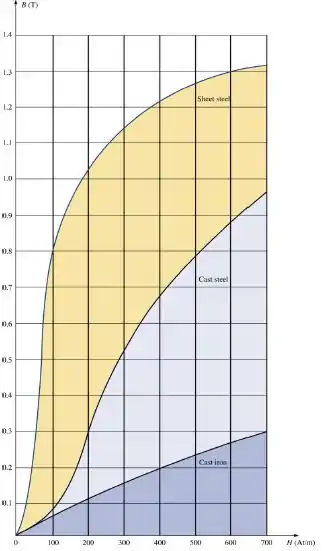
A curva de magnetização, também chamada de curva de histerese, desse núcleo é a de cor laranja, já que seu material é em aço laminado (Sheet steel). Então, analisando a curva de magnetização, temos que para essa densidade de fluxo a intensidade de campo magnético é:
Como, , a permeabilidade do núcleo no lado esquerdo é
Como eu disse antes, essa é a permeabilidade do lado esquerdo do núcleo. Então, essa será a permeabilidade das relutâncias e .
Passo 4
Com isso, podemos calcular as três relutâncias do lado esquerdo do circuito. Vamos começar por e :
Agora vamos calcular a relutância do entreferro:
Passo 5
Como já calculamos as relutâncias do ramo direito do circuito e o fluxo que passa por elas, vamos utilizar a analogia entre circuitos magnéticos e determinar a força magnetomotriz no nó do circuito.
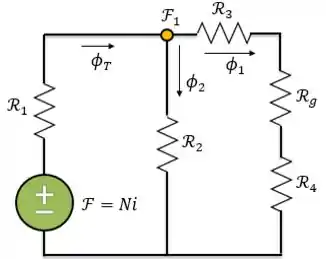
Passo 6
Também está sendo aplicado a relutância a mesma , já que esta relutância está em paralelo com o ramo da esquerda do circuito. Então:
Agora, vamos utilizar uma outra relação para na perna central:
Como e , podemos calcular a intensidade de campo magnético na perna central:
Então, analisando a curva de histerese, temos que para essa intensidade de campo magnético a densidade de fluxo é:
Com o valor da densidade de fluxo magnético podemos calcular o fluxo na perna central:
Passo 7
Como o fluxo magnético é análogo à corrente elétrica, temos que a soma dos fluxos que entram em um nó é igual à soma dos fluxos que sai desse nó.
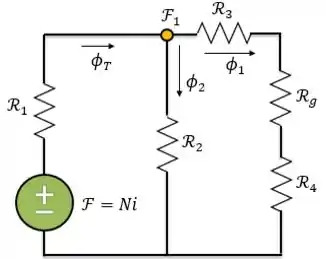
Logo, no circuito acima:
Passo 8
Também podemos calcular a permeabilidade da perna central do núcleo utilizando os valores encontrados para e . Como, , temos:
Agora já temos todos os valores necessários para calcular a relutância referente à perna central do núcleo:
Passo 9
Falta determinarmos a relutância , referente ao caminho . Para determinarmos seu valor, antes, temos que determinar a permeabilidade magnética do núcleo por onde passa o fluxo total :
Com o valor do fluxo total podemos calcular a densidade de fluxo magnético:
Então, analisando a curva de magnetização, temos que para essa densidade de fluxo a intensidade de campo magnético é:
Portanto, a permeabilidade do núcleo nessa região será:
Passo 10
Agora vamos calcular a relutância :
Passo 11
Para encontrarmos o valor da corrente na bobina, primeiro temos que determinar a força magnetomotriz .
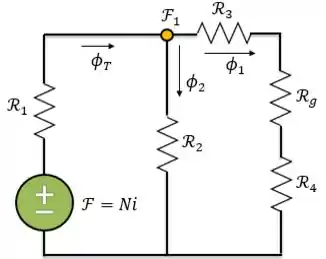
Podemos determiná-la de várias maneiras. Uma delas é determinar a relutância equivalente do circuito e utilizar a relação análoga a lei de Ohm:
Mas, podemos determiná-la de uma maneira mais rápida, já que:
Viu só?! Igual a gente fazia em circuitos elétricos!
Então, substituindo pelos valores que calculamos:
Passo 12
Como
A corrente será
Pronto!
Resposta