Um núcleo de transformador com comprimento efetivo de caminho médio de (polegadas) tem uma bobina de espiras enroladas em torno de uma perna. A área de sua seção reta é (polegadas quadradas) e sua permeabilidade magnética relativa é . Se uma corrente de estiver circulando na bobina, qual será o fluxo total no núcleo? Qual é a densidade de fluxo?
Passo 1
Para melhor visualização, fiz o desenho do circuito para você entender melhor o que está acontecendo:
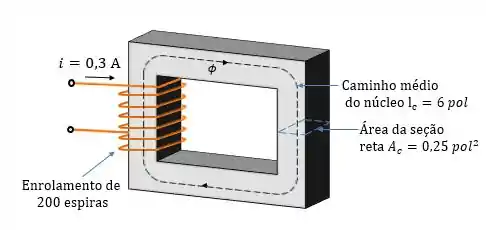
A força magnetomotriz do circuito será:
O circuito magnético associado à configuração acima é esse:
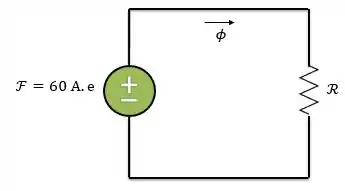
Passo 2
O próximo passo é calcular a relutância do circuito. Lembra da fórmula da relutância?
Antes teremos que calcular o valor de
Passo 3
As medidas têm que estar em metros:
Passando de polegada para metro:
Agora já podemos calcular a relutância:
Passo 4
Agora já é possível calcular o valor do fluxo:
Passo 5
Para calcular a densidade de fluxo a gente tem que lembrar dessa fórmula aqui: