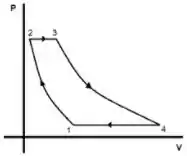
. O ciclo de Brayton é uma representação dos processos térmicos que ocorrem nas turbinas a gás, como as usadas na aviação. Suponhamos que se trata de moles de um gás ideal com . O ciclo se divide em etapas, incluindo uma compressão e uma expansão adiabáticas reversíveis, como mostra a figura abaixo:
Calcule o trabalho realizado em cada etapa do ciclo em termos das temperaturas nos
pontos e .
Calcule o rendimento do ciclo de Brayton.
Passo 1
Vem comigo que a gente vai detonar essa questão!
Temos em mãos um problema envolvendo máquina térmica.
O item pede o trabalho em cada etapa do processo. Vamos então ver o que temos em cada etapa do processo da máquina usando a primeira lei da termodinâmica.
Na primeira etapa temos um processo adiabático, , então temos que:
Na segunda etapa temos uma variação no volume a pressão constante, assim temos:
Na terceira etapa temos outro processo adiabático, , então temos que:
Na segunda etapa temos uma variação no volume a pressão constante, assim temos:
Para terminar de encontrar o trabalho em cada etapa vamos usar o fato de que para um gás ideal a energia interna é dada por:
E vamos usar também a equação dos gases ideais, dada por:
Para o item para encontrar o rendimento vamos usar a seguinte equação que nos fornece esse rendimento.
Onde é o trabalho total do processo e é o calor recebido pelo sistema que ocorre na etapa .
Vamos nessa então!
Passo 2
Começando com o item .
. Temos que:
. Temos:
. Temos que:
. Temos:
Prontinho, terminamos o item .
Passo 3
Agora vamos para o item . Temos que o rendimento é dado por:
Vamos primeiro encontrar o trabalho total, é dado por:
Temos então:
Então temos:
Agora temos que o calor recebido pelo sistema na etapa é dado por:
Então temos que o rendimento é:
Então temos que:
E com isso terminamos essa parte do problema!