Um gás ideal de coeficiente adiabático é submetido ao ciclo mostrado na figura, onde ab é um segmento de reta.
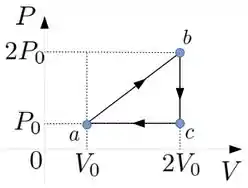
i) Calcule o trabalho e o calor no ciclo completo.
ii) Este ciclo representa um motor térmico ou um refrigerador? Justifique.
iii) Determine a temperatura do sistema nos pontos a, b e c.
iv) Considerando a maior e a menor temperatura, determine o rendimento de uma máquina de Carnot operando entre estes valores.
v) Determine o calor nos processos , e em termos das constantes (calor específico a volume constante) e R (constante universal dos gases). Indique se cada um deles é absorvido ou rejeitado pelo gás.
vi) Calcule o rendimento desta máquina térmica como função de . Este rendimento é maior ou menor que o de Carnot? Justifique a resposta com base nos cálculos obtidos.
Passo 1
i) Falou em ciclo termodinâmico, a gente já lembra logo que as funções de estado não variam num ciclo completo!
Lembrando a primeira lei da termodinâmica para o ciclo completo
Obtemos que
E como calcular o trabalho? É só calcular a área dentro do ciclo no diagrama P-V, ou, matematicamente:
Passo 2
A área do triângulo é
Passo 3
ii) Como o ciclo gira no sentido horário, no trabalho de maior módulo () ocorre um aumento de volume, logo o trabalho é positivo e o calor também.
Ou seja, o sistema absorve calor e realiza trabalho: a definição de um MOTOR TÉRMICO.
Passo 4
iii) Vamos calcular a temperatura em cada um dos pontos. Para isso, basta lembrar da equação dos gases ideiais:
Aplicando em cada ponto
Passo 5
iv) O rendimento de uma máquina de Carnot é:
Onde é a menor temperatura, , e a maior, .
Passo 6
v) Vamos calcular o calor nos processos:
No processo , a volume constante, o calor pode ser calculado como:
No processo , a pressão constante, o calor é:
Lembrando que e são relacionados da seguinte forma
O processo não temos nada constante, nem pressão nem volume nem temperatura, por isso, vamos ter que usar o calor do ciclo:
Como já temos tudo que precisamos basta substituir
Onde é absorvido e e são rejeitados pelo sistema.
Passo 7
vi) O rendimento do sistema é a razão entre o trabalho realizado () e o calor absorvido ().
Dividindo por R em cima e embaixo,
Temos que escrever isso em função de , lembre-se que
Substituindo no rendimento
E isso é maior ou menor que o rendimento de Carnot?
Pra testar vamos fazer
Se isso for satisfeito então é menor!
Como , já que , então o nosso rendimento é menor do que o rendimento de Carnot!
Resposta
- Motor Térmico, pois e .
-
, ,
- , absorvido.
, rejeitado.
, rejeitado.