A máquina de Stirling funciona com um ciclo termodinâmico formado de 4 processos mostrados no diagrama ao lado. Os processos são isotérmicos enquanto são isovolumétricos.Suponha que a substância de trabalho são de um gás ideal diatômico e que o motor opera entre as temperaturas e (Quando necessário use e ).
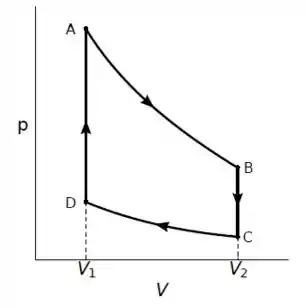
- Calcule, para o ciclo, o calor absorvido e o trabalho realizado pelo gás sabendo que
- Calcule a eficiência deste motor e compare com a eficiência de uma máquina de Carnot operando entre as temperaturas mais alta e mais baixa do ciclo. Expresse os resultados na forma de fração.
Passo 1
O calor é absorvido em processos onde há o crescimento da pressão ou do volume. Ou seja, em .
Em ocorre uma transferência à volume constante, ou seja:
Observe que foram colocadas as temperaturas das isotermas, pois elas coincidem com o final dos processos isovolumétricos. Além disso, perceba que usamos para o , já que o gás é diatômico.
Em relação ao processo , como o mesmo é isotérmico, vamos ter:
Para uma isoterma:
Assim:
Assim, o calor absorvido total vale:
Passo 2
Já o trabalho total vai ser a soma de todos os trabalhos:
Como ocorrem a volume constante:
Os outros dois trabalhos são calculados como trabalhos de isotermas, como fizemos antes. Já calculamos o
E o
Assim:
Passo 3
b)
A eficiência desse ciclo é dada por:
E o de Carnot:
Como:
Então:
Como era de se esperar.
Resposta
a)
b)