Em uma máquina de Stirling idealizada o fluido de trabalho (considerado um gás ideal) realiza as seguintes etapas reversíveis:
: Uma expansão isotérmica do volume ao volume à temperatura .: Um resfriamento a volume constante, atingindo a temperatura .: Uma compressão isotérmica à temperatura , reduzindo o volume de a : Um aquecimento a volume constante, de forma que o gás retorne ao seu estado inicial.
Expresse suas respostas em termos de , , e , da constante dos gases , do calor específico molar a volume constante e do número de moles do fluido.
- Esquematize o diagrama PV para este ciclo.
- Calcule o trabalho realizado em cada etapa deste ciclo.
- Calcule o calor transferido em cada etapa deste ciclo.
- Calcule a variação da entropia em cada etapa deste ciclo.
- Calcule a razão entre o trabalho total realizado no ciclo e o calor absorbido da fonte a temperatura e compare o resultado com a eficiência de um ciclo de Carnot operando entre as temperaturas e .
Passo 1
a):
Antes desenhar, vamos pensar um pouco:
Nos processos e , temos aquecimentos e resfriamentos à volume constante. Então sabemos que ali nós vamos desenhar retas paralelas ao eixo das pressões.
Os outros dois processos são transformações isotérmicas, então você já sabe que vão ter duas isotermas ali. Então, ligando os pontos com as isotermas e as transformações a volume constante, o gráfico ficará assim:
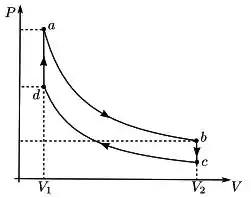
Passo 2
b):
Onda existe realização de trabalho nesse ciclo? Onde há variação de volume! Então sabemos que não pode acontecer em e . Ali, como os volumes são constantes, o trabalho é igual a zero.
Logo, o trabalho ocorre nas transformações isotérmicas.
Vamos calcular primeiro o trabalho de :
O trabalho sempre é dado por:
Fazendo:
Logo:
No caso desse processo, , e :
Pro processo a coisa fica bem parecida, só que no caso . e :
Passo 3
c):
Vamos analisar primeiro o processo
Como a temperatura é sempre a mesma, a variação de energia interna, que é uma função da temperatura, é nula. Isso sempre acontece: Quando a variação de temperatura é nula, a variação de energia interna também é. Então, pela primeira lei da termodinâmica:
Logo:
Aqui a gente calcule a troca de calor através da expressão básica do calor:
Podemos usar ou ou , dependendo do caso. Como a transformação é a volume constante, usamos . Então:
Aqui, novamente, por se tratar de uma transformação isotérmica:
De novo uma transformação isovolumétrica. Logo:
Passo 4
d):
Vamos calcular primeiro a variação da entropia em . Como ali a temperatura é constante, vamos poder tirá-la pra fora na integral. Vamos ver:
No caso, temos uma transformação isovolumétrica. A equação da variação de entropia será:
O que fizemos ali foi
Continuando:
O processo vai ser parecido com o processo , já que ambos são isotérmicos. Então:
Novamente fazemos:
Passo 5
e):
A eficiência será dada por:
O trabalho total será a soma dos trabalhos que a gente encontrou:
Já o calor que vem da fonte quente é dado por:
Logo:
Agora vamos comparar isso com uma máquina de Carnot operando entre as duas temperaturas...:
A eficiência pra uma máquina de Carnot operando entre uma fonte quente com temperatura e uma fria de temperatura é dada por:
Sendo e
Ou seja, a máquina tem a mesma eficiência que uma máquina de Carnot.
Resposta
a):
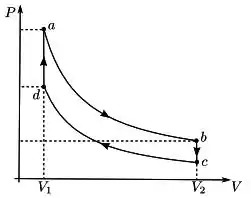
b):
c):
d):
e):
A mesma eficiência que a do ciclo de Carnot.