Ciclos Termodinâmicos e Máquinas Térmicas, Segunda Lei da Termodinâmica, Primeira Lei e Gases Ideais
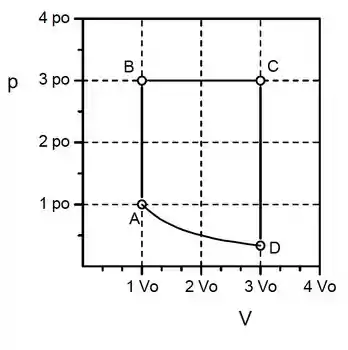
O motor de Haugse pode ser aproximado pelo ciclo mostrado na figura. Suponha que o ciclo seja efetuado por um mol de um gás ideal diatômico e que os valores de e sejam conhecidos. Deixe as respostas em termos de , e .
e são processos isométricos, é isobárico e o processo é isotérmico.
Calcule o calor fornecido ao gás no processo .
Calcule o trabalho total gerado pelo ciclo.
Calcule a variação de entropia entre os pontos e .
Calcule a eficiência deste motor.
Compare a eficiência com a máquina de Carnot operando entre as temperaturas e . Comente.
Passo 1
Vamos calcular a troca de calor em cada processo. No processo , temos um transformaçãoo isométrica, portanto o calor trocado pode ser definido por:
Lebrando que por ser diatômico, temos que . Vamos agora determinar a temperatura em e em função dos parâmetros conhecidos. Usando a lei dos gases ideais, temos, em :
Em , temos:
Substituindo na equação para o calor, temos:
Passo 2
No processo , temos uma transformação isobárica, portanto, podemos definir o calor como:
Lembrando que , por se tratar de um gás diatômico! Vamos agora determinar a temperatura em :
Substituindo na equação para o calor, temos:
Portanto, o calor total recebido no processo é:
Passo 3
Sabendo que nos processos isovolumétricos o trabalho realizado é zero, precisamos apenas calcular o trabalho realizado em e em . Vamos começar com , por ser um processo isobárico, temos:
Passo 4
Agora vamos analisar o processo . Por se tratar de um processo isotérmico, temos, pela primeira lei da termidinâmica:
Sabendo que e substituindo na equação para o trabalho, temos:
Portanto o trabalho gerado no ciclo é:
Passo 5
Para calcular a variação de entropia entre os pontos e , vamos trabalhar com cada processo em separado. Vamos começar com o processo . Pela definição de entropia, temos:
Por ser um processo isométrico, temos que:
substituindo, temos:
Sabendo que por ser um gás diatômico , que e , temos:
Passo 6
Utilizaremos o mesmo procedimento para o processo . Por ser um processo isobárico, temos que:
Desse modo a entropia fica:
Sabendo que e substituindo as temperaturas para em função dos parâmetros conhecidos, e , temos:
Ou seja a entropia entre os pontos e é:
Passo 7
Para calcular a eficiência do motor, vamos relembrar da fórmula:
Pelos processos que descrevem o ciclo, podemos perceber que o calor é recebido nos processos e , podemos perceber isso pela primeira lei da termodinâmica. Portanto o calor recebido da fonte quente é:
Só para não ficar dúvidas, o processo , por ser isométrico, tem trabalho igual a zero, ou seja , como a temperatura está diminuindo, energia interna é negativa, e por consequência o calor também, portanto, nesse processo, o calor é rejeitado.
No processo , por ser isotérmico, temos que a variação de energia interna é zero, ou seja , como temos que o trabalho é negativo e podemos ver isso pelo diagrama. O calor também é negativo e portanto, é rejeitado durante esse processo.
Voltando ao cálculo da eficiência, como temos o calor recebido e o trabalho realizado a cada ciclo , pois já calculamos anteriormente, a eficiência fica:
Passo 8
Para um ciclo de Carnot, temos que a eficiência é dada por:
Para as temperaturas obtidas, temos:
Substituindo pelas temperaturas em função dos parâmetros conhecidos, temos:
Podemos perceber, como já era de se esperar que o ciclo de Carnot teria eficiência maior, trabalhando entre as mesmas temperaturas.
Resposta
. O ciclo de Carnot, trabalhando entre as mesmas temperaturas apresenta eficiência maior.