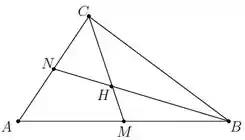
Considere três pontos não colineares , e , o ponto médio do segmento , , o ponto médio do segmento , , e o ponto comum aos segmentos e , .
a) Escreva como combinação linear de e .
b) Escreva como combinação linear de e .
c) Mostre que e .
Passo 1
a) A gente sabe, por soma de vetores, que . Sabendo que é ponto médio de , podemos escrever assim:
Como é a mesma coisa que , temos que
Boa!! Já temos em função de e , agora é só simplificar:
Passo 2
b) O esquema aqui é bem parecido com a letra a, olha:
Passo 3
c) Como e são paralelos, temos que enquanto, analogamente,
Belezinha, agora, sabendo que , substituindo:
Substituindo as expressões encontradas nos itens anteriores:
Passando pro lado direito:
Como e são L.I., seus coeficientes só podem ser :
De temos que . Substituindo em , temos
Logo, e
Resposta
a)
b)
c) Demonstração.