Funções de Várias Variáveis, Curvas Parametrizadas
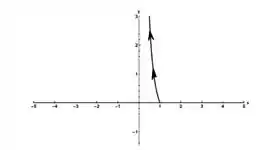
Considere a curva com
- Mostre que a imagem de está contida numa curva de nível da função e determine o nível.
- Esboce a imagem de indicando o sentido do seu percurso.
Passo 1
- Pra gente confirmar que a curva está contida numa curva de nível de , temos que fazer a substituição das coordenadas e da curva na função . Temos que:
- Vamos esboçar ? Bom, é uma ótima ideia se a gente começar esboçando a própria curva de nível (gastaremos menos neurônios fazendo assim)
Passo 2
Colocando esses e na função, fica assim:
Como ...
Beleza!! Conseguimos descobrir que o nível da nossa curva é !!
Isso prova que a curva está de fato contida na função , sendo parte da sua curva de nível .
Passo 3
Como o nível da curva é , basta colocar esse valor para o , que fica:
Passo 2
Perfeito, agora que temos a curva, é só esboçá-la :) Não que isso seja sempre fácil, mas convenhamos, todos sabemos que é a hipérbole:
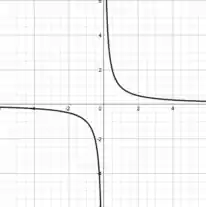
Tudo o que você tem que pensar agora é: Estamos elevando esse ao quadrado, então a curva nunca terá valores negativos! Aí pegamos essa parte da esquerda e refletimos ela pra cima, pegou a ideia? Assim, o gráfico de é:
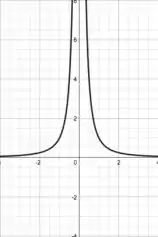
Passo 3
Agora você me pergunta, mas e o ?? Não era ?
Calma! Tudo o que temos que fazer é transladar (nome bonito para pegar de um canto e botar no outro) cada ponto da curva uma unidade para baixo (no sentido negativo do eixo ). É como fingir que o eixo caiu pra posição :
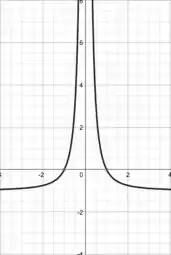
Passo 4
Perfeito! Agora é só analisar qual é o intervalo que a nossa curva aparece.
Sabemos que . Quando varia entre e , o varia entre e , isso vai fazer o valor de ir de à , isso vai nos dizer o sentido dessa curva, temos que pegar a parte onde varia entre e e colocar ele indo do até o .
E fazendo o mesmo para , vemos que ela varia entre e .
Assim, pegamos a seção correspondente na curva , com o entre e , e o entre e
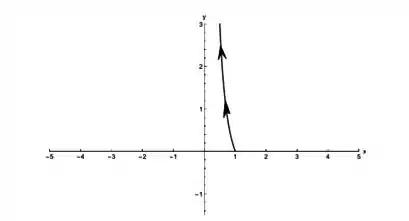
(imagem retirada do gabarito oficial)
Resposta
a) O nível é 1.
b) 