Seja
a) Determine o domínio da função e esboce seu gráfico.
b) Encontre a curva de nível da função que contém o ponto .
c) Dê uma parametrização para a curva do item .
Passo 1
a)
A função é definida por uma raiz quadrada, ou seja: o termo dentro dela não pode ser negativo! Assim, a é definida na região
Dividindo tudo por 24:
Passo 2
Portanto, o domínio da função é o interior da elipse dada pela equação
É uma elipse centrada na origem e cujos semieixos valem no eixo , e no eixo .
Saca só a cara dela:
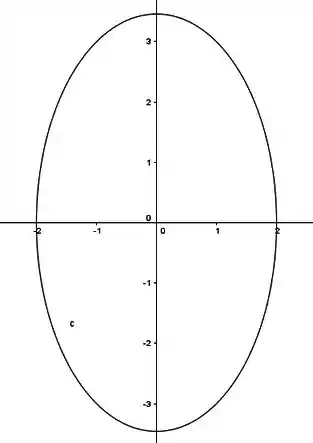
Passo 3
Tranquilo, achamos o domínio, mas agora precisamos esboçar o gráfico.
Vamos elevar isso ao quadrado (mas não podemos esquecer depois que ):
Isso tá com uma cara de elipsoide, de equação característica
Passo 4
Então vamos dividir tudo por 24, o que dá:
Realmente, isso é a equação de um elipsoide, com e .
Passo 5
Isso significa que se cortarmos o gráfico da função com planos paralelos aos planos coordenados vamos obter elipses.
No plano temos
que é a seguinte elipse:
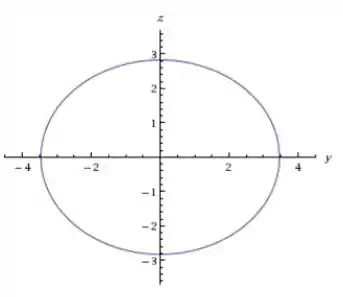
Passo 6
No plano temos
que é a elipse:
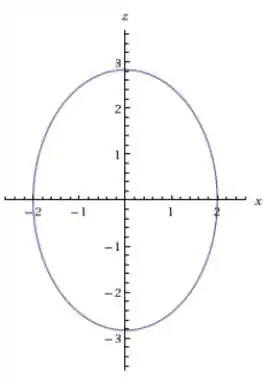
Passo 7
Por fim, a interseção do gráfico com o plano é a elipse
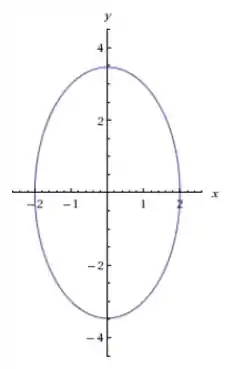
Passo 8
Portanto, o gráfico que precisamos esboçar é a metade de um elipsoide (lembra que ?) cujas interseções com os planos coordenados são essas elipses que a gente viu aí em cima.
Aqui está nosso gráfico!
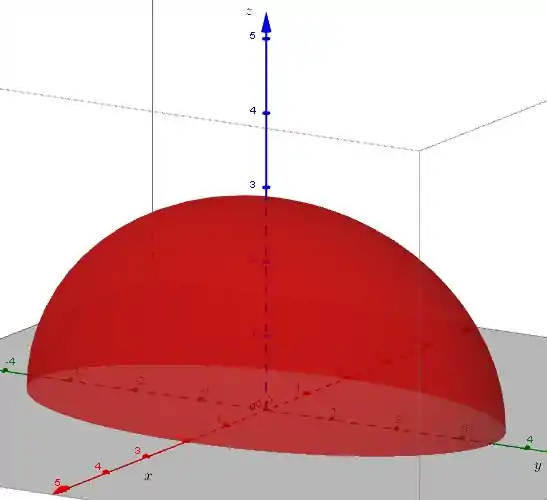
Passo 9
b)
Primeiro vamos determinar qual é o nível da curva de nível a qual o ponto pertence. Pra isso, vamos calcular o valor de em :
Beleza, então pertence à curva de nível de .
Passo 10
Agora vamos identificar essa curva, igualando a expressão da função a :
E isso, como era de se esperar, é a equação de uma elipse (é uma curva de nível de um elipsoide)!
Podemos botá-la na forma padrão dividindo tudo por 18:
Essa é a nossa curva !
Passo 11
c)
Vai que tá quase acabando! Agora só nos resta parametrizar essa elipse do item anterior. Tranquilo né?
Lembrando que tendo a equação de uma elipse na forma
podemos parametrizá-la assim:
Portanto, uma parametrização da curva é:
Pronto, só isso! :)
Resposta
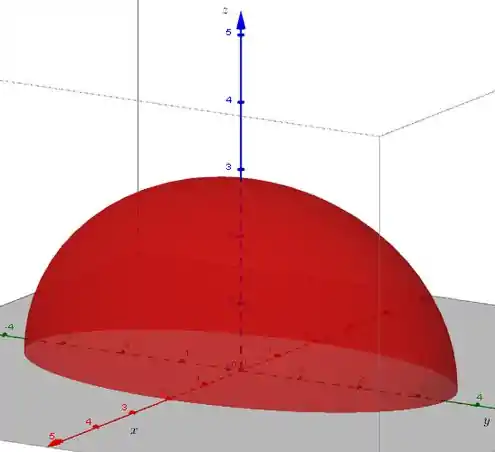
a)
Domínio:
Gráfico:
b)
A curva é a elipse
c)
Uma parametrização de é: