Seja . Considere as curvas de nível
e
a) Exiba uma parametrização da forma para , explicitando , e . E, ainda, calcule .
b) Exiba uma parametrização da forma , , para .
c)Encontre o(s) pontos de onde sua reta tangente é vertical.
d)Encontre o(s) pontos de onde sua reta tangente é horizontal.
e) Esboce e .
f) Encontre apenas um ponto de onde a reta tangente à neste ponto é paralela à reta . Dica: Levem em conta que é solução da equação e é solução de
Passo 1
a)
Vamos com calma, essa questão tem muito comando de uma vez XD Primeiro, antes de fazer interseção, vejamos que curva de nível é essa . Colocando , teremos:
Isolando o , temos a curva:
Passo 2
Beleza, agora podemos parametrizar essa curva. Se chamarmos de , teremos:
E a interseção, onde entra? Veja que a única condição que ela impõe é que esteja entre e ! E, como já é o próprio parâmetro, então, temos:
Agora, só de bobeira, vamos derivar essa curva (por que né, a questão pede…). Só derivar cada coordenada!
Passo 3
b)
Agora, como queremos que a primeira coordenada seja o parâmetro, vamos fazer o mesmo processo do passo anterior, mas isolando o :
Perceba aqui que , pois estamos dentro de uma raiz quadrada! Colocando como o parâmetro, a curva fica:
Agora, acrescentando a restrição, que diz que , então teremos:
E pronto, só isso :D
Passo 4
c)
Vamos lá! Queremos o ponto no qual a reta tangente é vertical, ou seja, paralela ao vetor , que é o vetor unitário da direção , certo?
Já calculamos o vetor tangente lá na letra , quando derivamos a curva, lembra? Ele é:
Assim, os pontos são todos aqueles que fazem esse vetor ser ! A segunda coordenada já vale , então só precisamos ver o que faz a primeira valer !
Para que isso aconteça basta que seja , certo? No nosso caso, a única restrição seria colocar pois zeraria o termo com expoente negativo. Enfim, é a nossa solução!
Colocando em , teremos:
Passo 5
d)
Para ver os pontos que fazem a reta tangente ser horizontal, já não podemos mais usar aquela parametrização , pois a segunda coordenada de sua derivada é sempre !
Neste caso, podemos pensar o seguinte: Se o vetor gradiente é normal à curva de nível, e se o vetor tangente a essa curva é paralelo ao vetor (pois a reta é horizontal), então o vetor gradiente é normal ao vetor , e, portanto, paralelo ao vetor !
O vetor gradiente para a função é:
E, para que ele seja , então , obrigatoriamente, certo? Colocando na curva de nível , teremos:
Ou seja, ! E, assim, nossos pontos são e :)
Passo 6
e)
Missão dada é missão cumprida! Partiu esboçar essas curvas de nível! Para a primeira, de nível , temos:
Isolando o , teremos:
Como essa equação veio de , então temos que não pode ser menor do que , pois nenhum número ao quadrado vai dar outro negativo ;)
Sendo assim, essa curva tem o molde parecido com o de uma parábola, e tem simetria em relação ao eixo por causa desse . Lembrando que deve ser maior ou igual a , fica algo assim:
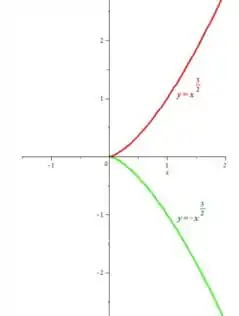
Passo 7
Agora, esbocemos a curva de nível ! Ela é:
Beleza, e agora? Vamos ter que dar um jeito de esboçar isso.
Lembra do teste das derivadas? Vamos examinar onde temos pontos críticos para a curva :
Aqui, para essa derivada ser , então , certo? Neste caso, temos, para o ,
Se a gente estivesse na parte , então a derivada seria:
E, para ela ser , então . Assim, teríamos,
Show? Temos dois pontos simétricos em relação ao eixo ! Enfim, para a curva de nível , temos pontos críticos em e .
Passo 8
Agora, vejamos as segundas derivadas. Podemos encontrar a segunda derivada de e depois só trocar o sinal, se for necessário, para ver a de . Para a primeira parte, fica:
Podemos multiplicar em cima e embaixo por , e teremos:
Fazendo as distributivas no numerador, teremos:
Calma, eu sei que tá feito. Na verdade, isso está horrível D:
Mas acho que essa segunda derivada na qual chegamos já tem uma informação valiosa: temos em todos os termos do numerador, e, assim, se colocarmos , então a segunda derivada será zerada!
Isso significa que temos pontos de inflexão em ! Como vimos, quando nessa curva de nível, ! Logo, os pontos de inflexão ocorrem em e .
Passo 9
Será que já podemos esboçar alguma coisa? Vejamos o que temos: Sabemos que o vetor tangente à curva é horizontal quando , e vertical quando . Sabemos, também, que é quando que temos dois pontos de inflexão, em e . Sabemos, ainda, que esses mesmos pontos batem com os pontos críticos, pois é quando o vetor tangente é horizntal!
E, olhando para a curva , percebemos que quanto maior o , maior ela, é, ou seja, a medida que cresce a partir do momento que se torna positivo, cresce também! Lembrando que também temos a “parte de baixo”, quando cresce em , descresce! Juntando tudo isso, teremos, por fim, algo parecido com:
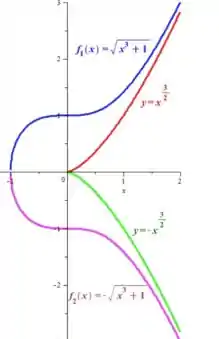
Passo 10
f) Primeiro, é bom parametrizarmos a reta , para visualizar mais facilmente seu vetor diretor :) Isolando o , teremos:
Usando o como parâmetro, teremos a reta
Como o vetor diretor da reta é aquele formado pelos coeficientes do parâmetro em cada coordenada, então o vetor diretor dessa reta é o , show?
Sabemos que o vetor gradiente é normal à curva de nível, logo, é normal ao vetor tangente à essa curva. Assim, o que querermos é encontrar o ponto no qual o vetor gradiente é paralelo ao vetor normal de , então esse será o ponto no qual o vetor tangente é paralelo ao vetor !
Para encontrar o vetor normal do vetor , basta trocar as coordenadas de lugar e trocar o sinal. Assim, temos:
Chegamos então que o vetor gradiente deve ser paralelo ao vetor :D Sei que isso parece confuso, então, leia devagar!
Passo 11
Ok, agora que sabemos que o vetor gradiente deve ser paralelo ao vetor , podemos escrever que:
Ou seja, um é múltiplo do outro. Colocando o vetor gradiente da nossa função, que já foi calculado, fica:
Igualando cada coordenada, temos:
Da segunda, temos que . Colocando isso na primeira, teremos:
Agora, podemos colocar essa relação na equação da curva de nível, e teremos:
E aí você me pergunta, qual é a solução dessa equação?! E eu digo: ainda bem que foi dada no enunciado! Falando sério, zoaram essa questão... nada nem um pouco intuitivo o.O
Mas vamos lá, o enunciado diz que podemos usar que é uma solução dessa equação, então a gente acredita. Substituindo-se na equação , teremos:
E, portanto, e o ponto pedido é !
Ufa! Demorou mas acabou!
Resposta
a) e
b)
c)
d) Pontos são e
e) 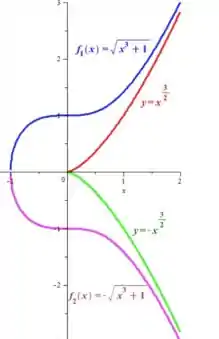
f) O ponto é