Sejam e . Esboce a imagem de e mostre que ela está contida em uma curva de nível de , indicando qual é o nível.
Passo 1
Vamos pelo mais simples, mostrar que é curva de nível de , beleza? Se isso for verdade, então para qualquer , devemos ter que .
Partiu substituir em !
Como a secante é o inverso do cosseno, então , e
Ou seja, a curva é de nível ! Show, apenas isso!
Passo 2
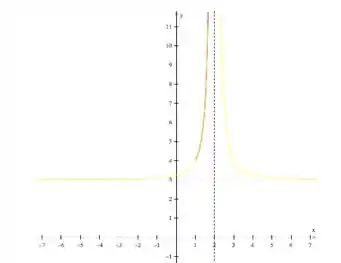
Vamos agora esboçar essa curva. Sua equação é:
No plano , temos, portanto:
Levando em conta, novamente, que , então , e
Para esboçar essa curva, agora, devemos perceber algumas características dela, como:
- Quando , o parte pra infinito, ou seja, temos uma assíntota vertical em
- Como é sempre positivo, então é sempre positivo
- Como quando ou tende a , então o menor valor que assume é
Com isso, podemos ter uma ideia da curva, que parte pra infinito nos dois lados da reta e decai para quando vai para mais ou menos infinito:
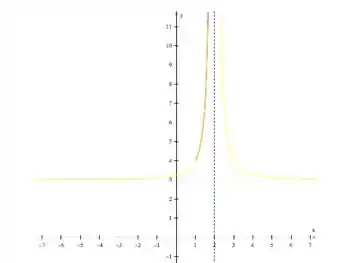
Resposta
A curva tem nível e seu esboço é:
Exercícios de Livros Relacionados
Determinar o centro e o raio das seguintes circunferências e depois escrever uma equação vetorial para cada uma.c) x 2 + y 2 + 5 y - 2 = 0
Determinar uma representação paramétrica da reta representada por:b) 2 x - 5 y + 4 z = 1 ,3 x - 2 y - 5 z = 1
Encontrar uma equação vetorial das seguintes curvas:f) y = x ,z = x 2 + y 2
Encontrar uma equação vetorial das seguintes curvas:m) x 2 + y 2 = 1 ,z = 2 x - 2 y
Encontrar uma equação vetorial das seguintes curvas:d) y = x 1 2 ,z = 2