Considere a função
- Represente geometricamente o domínio de e faça um esboço da curva de nível que passa pelo ponto .
- Encontre um intervalo e uma função contínua cuja imagem é .
Passo 1
a)
Vamos então representar o domínio da função! Como deve saber, temos uma listinha de coisas que merecem atenção, e agora podemos ver dois casos, a princípio:
- O denominador da fração não pode valer
- O valor dentro da raiz que tá no denominador tem que ser (ser menor do que não dá, por que é uma raiz, e , até poderia ser, mas ela está no denominador!)
Passo 2
Juntando o que conseguimos no primeiro passo, teremos então:
Assim devemos ter, ou as duas parcelas dessa multiplicação sendo positivas, ou as duas parcelas dessa multiplicação sendo negativas.
Ou
Legal! Agora que temos a condição pra nossa função existir, vamos dar uma olhadinha no que isso quer dizer graficamente?
Passo 3
A primeira coisa que eu costumo fazer quando tenho uma desigualdade é trocar ela por um sinal de “igual” e ver do que estamos tratando. Veja, se fosse:
Essas são as duas retas que temos tanto na primeira quanto na segunda região;
Teríamos aquele par de retas que passam bem no meio do primeiro e terceiro quadrantes, e segundo e quarto quadrantes. Olha só, em vermelho a reta e em azul a :
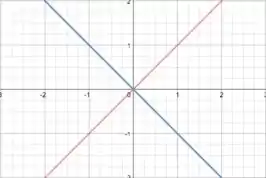
Agora vamos colocar o sinal de desigualdade!
Veja só, se temos que e , isso quer dizer que, tanto para a reta quanto para a , o que vale é a parte do plano abaixo de cada uma delas.
Veja só, se temos que e , isso quer dizer que, tanto para a reta quanto para a , o que vale é a parte do plano acima de cada uma delas.
Portanto, nosso domínio a região acima das retas e abaixo das retas (a parte roxa e a parte branca do gráfico):

Passo 4
Agora, vamos traçar a curva de nível do ponto ? É só a gente substituir esse ponto na equação de , ver qual é o valor do nível, depois analisar a curva sem substituir o ponto, mas substituindo o nível. Veja só:
Passo 5
Agora, colocamos como sendo o valor para o nível:
Desenvolvendo a equação, vamos elevar os dois lados ao quadrado. Mas aqui temos que observar o seguinte: o valor da raiz continua não podendo ser menor ou igual a !
Completando o quadrado para o , somando de cada lado:
Reescrevendo o termo do quadrado do :
Veja que estamos cada vez mais próximos da equação de uma elipse! Vamos continuar... temos que passar o coeficiente do pro denominador. Vai fica:
E podemos tirar esse denominador do parêntesis elevando-o ao quadrado:
E agora dividimos tudo por , ficando:
Ufa! Demorou mas saiu! Temos, enfim, a equação da curva de nível, que é uma elipse! Se não tiver muito bem lembrado, só comparar com a equação geral:
Passo 6
Agora é só esboçar a curva! Como podemos ver:
Ela está centrada em , pois e .
Mas, lembrando que o nosso domínio é limitado pelas pelos semiplanos , temos que verificar de que forma isso afeta no desenho da elipse! Então, vamos arbitrariamente substituir na equação dela, (estamos fazendo assim pra evitar excesso de conta, já que só temos um , que está ao quadrado)
Com (tanto faz, mais ou menos, está ao quadrado!), teremos:
Resolvendo a equação do segundo grau,
E o que esse valor significa? Ora, acabamos de encontrar o valor para a interseção entre a nossa elipse e as retas , ou se preferir, . Como temos que a função existe apenas para valores acima dessas retas, nossa elipse só existe para valores acima de !
Passo 7
Agora estamos aptos a desenhar essa elipse! Já sabemos que ela não existe para valores menores que . Então, vamos olhar para os denominadores de e . Como o denominador de é , então a medida do eixo maior é . Como o denominador de é , então a medida do deixo menor é ! E como ela está centrada em , todos os pontos foram deslocados em no sentido positivo do eixo , logo, seu máximo que era em , agora é em .
E, enfim, aqui vai o desenho da elipse:
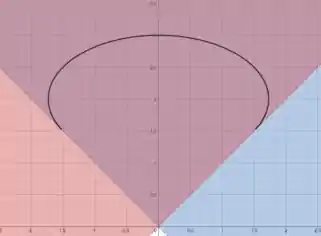
Veja que quando está prestes a atingir o valor de , a elipse já não existe mais.
Passo 8
b)
Esse enunciado é meio doido né? Deixa eu te explicar o que ele quer! Esse negócio de significa que queremos uma função em que damos um valor do intervalo e recuperamos uma dupla de valores no plano.
Que tipo de função faz isso? Pega um valor e leva em dois valores do plano? A parametrização de uma curva faz isso!
Então na verdade ele quer a parametrização daquela elipse do passo anterior, essa será e o intervalo são os valores que pode assumir!
Vamos agora determinar uma parametrização para essa elipse?
Bom, na verdade não tem nada demais. É basicamente parametrizar uma elipse como outra qualquer e depois restringir o domínio do parâmetro!
Veja, se para uma elipse genérica teríamos a parametrização:
Então para a nossa elipse teremos:
E, como , então,
Assim, nossa parametrização fica sendo:
Resposta
O domínio é a parte roxa e branca.
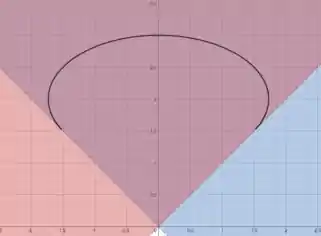
Essa é a representação geométrica de
