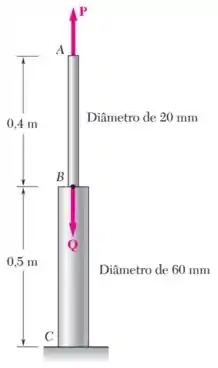
Ambas as partes da barra são feitas de um alumínio para o qual . Sabendo que a intensidade de é , determine o valor de de modo que o deslocamento em seja zero e o deslocamento correspondente de .
Passo 1
Se o trecho da barra sofrer uma variação de comprimento e se o trecho da barra sofrer uma variação de comprimento , então o deslocamento do ponto vai ser a soma dessas variações:
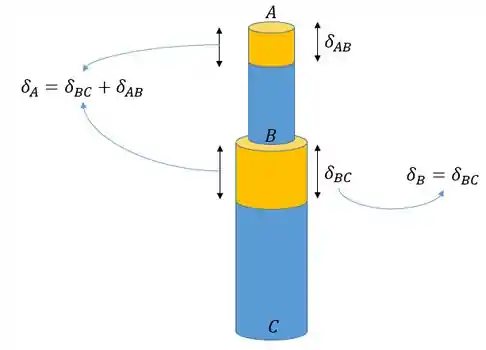
Essas variações de comprimento podem ser calculadas usando a fórmula:
Para tanto, vamos precisar:
- Das forças normais em cada trecho da barra, calculadas em função das forças e através de uma análise dos esforços internos em cada trecho;
- Dos comprimentos originais de cada barra, e , de acordo com a figura do exercício;
- Do módulo de elasticidade do material da barra;
- E das áreas das seções transversais de cada trecho da barra, calculadas a partir de seus diâmetros e , de acordo com a figura.
Ok, e o que é que o exercício quer?
No item , ele quer saber qual deve ser o valor da força tal que o deslocamento em seja zero:
Aí a gente olha na nossa equação do deslocamento de e vê o seguinte:
O que significa que uma variação tem que ser igual ao oposto da outra:
Isso só vai acontecer se uma barra estiver tracionada e a outra comprimida! Dessa forma os deslocamentos podem sim se anular.
Mas nós podemos encontrar essas variações em função das cargas e nas barras!
(Primeiro temos que encontrar as forças internas em função de e e usar a fórmula .)
Então desenvolvendo essa última equação, podemos encontrar qual é o valor da força tal que o deslocamento em seja zero.
Em seguida, no item , o exercício quer que a gente use o valor encontrado de para calcular o deslocamento do ponto , que vai ser igual a de comprimento do trecho :
Passo 2
Primeiro, temos que fazer uma análise dos esforços internos na barra para encontrar o valor da força normal em cada trecho.
Para as seções entre e , o desenho fica assim:

Aplicando o equilíbrio de forças, temos:
O que implica que:
E agora para o trecho , o desenho fica assim:
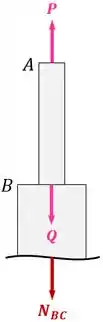
Aplicando o equilíbrio de forças:
Isolando , encontramos:
Passo 3
Como vimos anteriormente, para que o deslocamento em seja zero () é preciso que:
Agora que já temos as forças normais nos trechos e da barra, já estamos prontos para desenvolver essa expressão e descobrir qual é o valor de que garante essa condição.
Aplicando a fórmula para cada trecho, temos:
Não sabemos o valor das áreas das seções transversais da barra.
Mas sabemos que essas áreas são circulares e podem ser calculadas em função de seus diâmetros através da fórmula .
Sendo assim, a equação anterior fica assim:
Cortando os termos em comum dos dois lados, isso fica assim:
Substituindo as expressões encontradas para as forças normais e , temos:
O que é o mesmo que:
Queremos encontrar , então devemos isolá-lo:
Primeiro, isolamos :
E depois isolamos o próprio :
Colocando em evidência, isso fica assim:
Substituindo e substituindo os valores dos diâmetros e dos comprimentos fornecidos pela figura do exercício, temos:
Calculando tudo, isso dá:
Que é a resposta do item !
Passo 4
Para o item , vamos usar o valor encontrado para no item para calcular o deslocamento do ponto , que é igual à variação de comprimento do trecho :
Usando a fórmula para o trecho :
Descrevendo a área em função de seu diâmetro :
Como :
Substituindo os valores de , , , e :
Como , as unidades e vão se cortar e o resultado vai sar em (metros).
Calculando tudo:
Esse número é bem pequeno, então é uma boa reescrever ele em :
Ou seja, o ponto se deslocou para baixo.