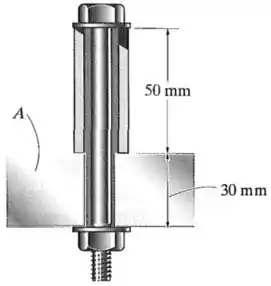
O parafuso de de diâmetro é feito de uma liga de alumínio e está instalado em uma luva de magnésio com diâmetro interno de e diâmetro externo de . Se os comprimentos originais do parafuso e da luva forem e , respectivamente, determine as deformações na luva e no parafuso se a porca do parafuso for apertada de tal modo que a tensão no parafuso seja de . Considere que o material em é rígido.
, .
Passo 1
O que está acontecendo?
Quando as porcas são apertadas, elas comprimem a luva e o material rígido.
Como reação, a luva e o material rígido empurram as porcas de volta, o que gera uma tração no parafuso.
Como essa tração e essa compressão são um par ação-reação, elas tem a mesma intensidade.
Agora...
O enunciado do exercício fala que a “tensão” no parafuso é de ...
Sabendo que o parafuso vai ser tracionado nesse sistema parafuso/porca, podemos concluir que deve ser na verdade a força de tração no parafuso.
E se o nosso parafuso está sendo tracionado por uma força de , isso significa que a nossa luva está sendo comprimida por uma força de .
E o que é que o exercício quer?
Ele quer saber o valor das deformações do parafuso e da luva.
Da Lei de Hooke, temos que:
Isolando , isso fica assim:
E como é a tensão normal média nas peças, então:
Agora vamos ver...
A tração de gera no parafuso uma força interna normal e a compressão de na luva gera nela uma força interna normal .
As áreas das seções transversais e podem ser calculadas a partir do diâmetro do parafuso e dos diâmetros internos e externo da luva e .
E ainda conhecemos os módulos de elasticidade do parafuso e da luva .
Então podemos usar essa última fórmula para calcular as deformações !
Passo 2
Aplicando a fórmula , que encontramos a partir da Lei de Hooke e da fórmula da tensão normal média, para o parafuso, temos:
A área da seção transversal do parafuso, que é circular, pode ser calculada a partir de seu diâmetro através da fórmula , então:
Substituindo os valores , e :
, então todas as unidades dessa equação vão se cortar.
Calculando tudo, encontramos:
Se quisermos, podemos dar uma unidade para qualquer resultado de deformação , como ou , mas isso não é necessário.
Passo 3
E agora aplicando a mesma fórmula para a luva:
A seção transversal da luva é como um anel, com um diâmetro externo e um diâmetro interno .
A sua área pode ser calculada como a diferença das áreas dos círculos formados por esses diâmetros. Como a área do círculo em função do diâmetro é , temos:
Substituindo os valores , , e :
Como , todas as unidades dessa equação vão se cortar.
Calculando tudo, isso dá: