O conjunto é composto por três hastes de titânio (Ti-6A1-4V) e uma barra rígida . A área da seção transversal de cada haste é dada na figura. Se uma força de for aplicada ao anel , determine o ângulo de inclinação da barra .
Dados:
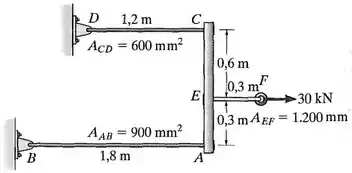
Passo 1
A primeira coisa que vamos fazer nesse exercício é desenhar um diagrama de corpo livre da barra rígida (como o da imagem abaixo) e aplicar as condições de equilíbrio nela.
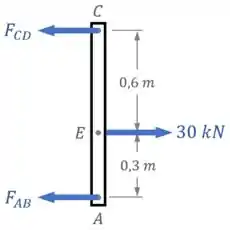
Com isso, vamos poder descobrir os valores das forças e que as hastes e fazem na barra rígida em função da força de que a haste faz.
Como reação a essas forças e , a barra faz trações de mesma intensidade nas hastes:
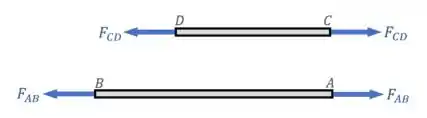
E assim, as forças internas normais nas hastes vão ser iguais à essas trações e :
Conhecendo as forças normais nas hastes, e identificando no enunciado e na figura:
- Os comprimentos iniciais e das hastes;
- O módulo de elasticidade do material das hastes;
- E as áreas e das seções transversais das hastes,
vamos poder usar a fórmula abaixo para encontrar as variações de comprimento e nas hastes:
Obs: Essa fórmula é aquela vem da união da Lei de Hooke com as fórmulas da tensão normal média e da deformação normal !
Sabendo as variações de comprimento e , vamos poder desenhar a nova configuração da barra e usar esse desenho para encontrar o ângulo de inclinação da barra, que é o que o exercício quer!
Passo 2
Começando pelo Diagrama de Corpo Livre da barra :
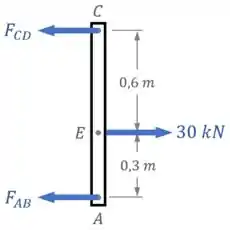
Duas condições de equilíbrio podem nos ajudar a relacionar essas forças aqui: o equilíbrio de momentos em relação a um ponto (vamos escolher o ponto ) e o equilíbrio de forças na horizontal:
Quanto ao somatório de momentos em relação ao ponto :
A força vai gerar um momento no sentido anti-horário () com um braço de .
Já a força de vai gerar um momento no sentido horário () com um braço de .
Sendo assim, o somatório de momentos fica assim:
Isolando , temos:
O que dá:
E quanto ao somatório de forças na horizontal, temos:
Isolando :
Encontramos que , então:
Por último, observando as hastes:
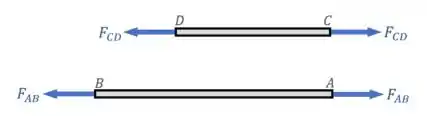
Vemos que elas estão sob tração pura, o que significa que a força interna normal em cada haste vai ser igual à força de tração em cada haste:
Passo 3
Agora que sabemos o valor das forças normais nas hastes, podemos aplicar a fórmula para encontras as variações de comprimento em cada haste.
Para a haste , temos:
Substituindo todos os valores:
, então as unidades e vão se cortar e o resultado disso tudo vai sair em metros ():
Fazendo tudo de novo para a haste , temos:
Passo 4
Determinadas as variações de comprimento de cada haste, podemos desenhar a nova configuração da barra .
Como os pontos e das hastes estão fixos, então toda a variação de comprimento das hastes implicou no deslocamento dos pontos e .
Na imagem abaixo, os pontos originais são e , os pontos deslocados são e , e as variações e são o deslocamento que houve entre esses pontos:
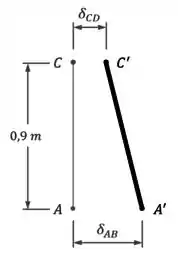
Agora, queremos saber o ângulo de inclinação da barra rígida em sua nova posição .
Então vamos definir o ângulo entre a inclinação antiga (vertical) e a inclinação nova como .
Esse ângulo vai fazer parte de um triângulo retângulo em que:
1. O cateto adjacente vai ser a distância vertical entre e , que vamos dizer que é igual à distância vertical de entre e ;
(Essa aproximação é aceita e necessária em exercícios desse tipo!)
& 2. O cateto oposto vai ser a diferença entre os deslocamentos de e , e .
Como mostra a imagem abaixo:
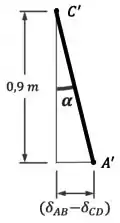
Desse desenho, conseguimos tirar que:
Substituindo e :
Isolando , temos:
O que dá: